题目内容
 实数a、b、c在数轴上的位置如图所示,化简下列代数式的值
实数a、b、c在数轴上的位置如图所示,化简下列代数式的值| a2 |
| (c-a+b)2 |
| 3 | b3 |
考点:二次根式的性质与化简,实数与数轴
专题:
分析:根据数轴得出<b<0<c,|c|>|a|>|b|,根据二次根式的性质得出|a|-|c-a+b|+|b+c|-b,去掉绝对值符号后合并即可.
解答:解:∵从数轴可知:a<b<0<c,|c|>|a|>|b|,
∴原式=|a|-|c-a+b|+|b+c|-b
=-a-c+a-b+b+c-b
=-b,
故答案为:-b.
∴原式=|a|-|c-a+b|+|b+c|-b
=-a-c+a-b+b+c-b
=-b,
故答案为:-b.
点评:本题考查了二次根式的性质,绝对值,数轴的应用,主要考查学生的计算和化简能力.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列命题中,是真命题的是( )
| A、同位角相等 |
| B、同旁内角互补 |
| C、内错角相等 |
| D、对顶角相等 |
 如图,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,试判断△ABC与△AEG面积之间的关系.
如图,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,试判断△ABC与△AEG面积之间的关系. 如图,在△ABC中,AD是BC边上的高,且BC=5,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是
如图,在△ABC中,AD是BC边上的高,且BC=5,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是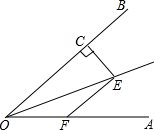 如图,∠AOE=∠BOE=22.5°,EF∥OB,EC⊥OB,若EC=1,则EF=
如图,∠AOE=∠BOE=22.5°,EF∥OB,EC⊥OB,若EC=1,则EF=