题目内容
如图，在△ABC中，AD是BC边上的高，且BC=5，AD=3，矩形EFGH的顶点F、G在边BC上，顶点E、H分别在边AB和AC上，如果设边EF的长为x（0＜x＜3），矩形EFGH的面积为y，那么y关于x的函数解析式是考点：相似三角形的判定与性质,根据实际问题列二次函数关系式
专题：
分析：设边EF的长为x（0＜x＜3），则AN=3-x，进而利用已知得出△AEH∽△ABC，进而得出EH的长，即可得出答案．
解答：
解：设边EF的长为x（0＜x＜3），则AN=3-x，
∵EH∥BC，
∴△AEH∽△ABC，
∴
=
，
∴
=
，
解得：EH=
（3-x），
∵矩形EFGH的面积为y，
∴y关于x的函数解析式是：y=
（3-x）×x=-
x2+5x．
故答案为：y=-
x2+5x．
解：设边EF的长为x（0＜x＜3），则AN=3-x，∵EH∥BC，
∴△AEH∽△ABC，
∴
| AN |
| AD |
| EH |
| BC |
∴
| 3-x |
| 3 |
| EH |
| 5 |
解得：EH=
| 5 |
| 3 |
∵矩形EFGH的面积为y，
∴y关于x的函数解析式是：y=
| 5 |
| 3 |
| 5 |
| 3 |
故答案为：y=-
| 5 |
| 3 |
点评：此题主要考查了相似三角形的判定与性质以及根据实际问题列二次函数解析式，根据已知得出EH的长是解题关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
如图（1）是长方形纸带，∠DEF=α，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），则图（3）中的∠CFE的度数是（ ）
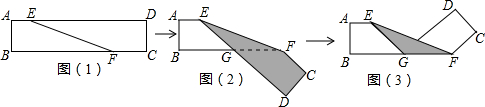
| A、2α |
| B、90°+2α |
| C、180°-2α |
| D、180°-3α |
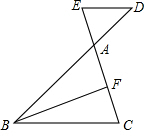如图，点D、E分别在△ABC的边BA、CA的延长线上，且DE∥BC，
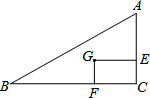如图，点G是Rt△ABC的重心，过点G作矩形GECF，当GF：GE=1：2时，则∠B的正切值为
实数a、b、c在数轴上的位置如图所示，化简下列代数式的值在平面直角坐标系xOy中，点P（2，1）关于y轴对称的点的坐标是（ ）
| A、（-2，1） |
| B、（2，1） |
| C、（-2，-1） |
| D、（2，-1） |
如果x+
=-3，那么3x+
=（ ）
| 1 |
| 2010 |
| 3 |
| 2010 |
| A、6 | B、-9 | C、3 | D、-1 |