题目内容
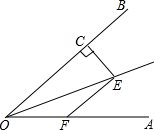 如图,∠AOE=∠BOE=22.5°,EF∥OB,EC⊥OB,若EC=1,则EF=
如图,∠AOE=∠BOE=22.5°,EF∥OB,EC⊥OB,若EC=1,则EF=考点:角平分线的性质,等腰直角三角形
专题:
分析:过点E作ED⊥OA于D,根据角平分线上的点到角的两边的距离相等可得DE=CE,再根据两直线平行,同位角相等求出∠EFD=45°,判断出△DEF是等腰直角三角形,然后根据等腰直角三角形的性质求解即可.
解答: 解:如图,过点E作ED⊥OA于D,
解:如图,过点E作ED⊥OA于D,
∵∠AOE=∠BOE=22.5°,EC⊥OB,
∴DE=CE=1,
∵EF∥OB,
∴∠EFD=∠AOB=22.5°×2=45°,
∴△DEF是等腰直角三角形,
∴EF=
DE=
×1=
.
故答案为:
.
 解:如图,过点E作ED⊥OA于D,
解:如图,过点E作ED⊥OA于D,∵∠AOE=∠BOE=22.5°,EC⊥OB,
∴DE=CE=1,
∵EF∥OB,
∴∠EFD=∠AOB=22.5°×2=45°,
∴△DEF是等腰直角三角形,
∴EF=
| 2 |
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,等腰直角三角形的判定与性质,平行线的性质,熟记各性质并作辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以下列长度的三条线段为边,可以构成三角形的是( )
| A、1,4,7 |
| B、2,5,8 |
| C、3,6,9 |
| D、4,6,8 |
下列长度的三条线段能组成直角三角形的是( )
| A、1,2,3 |
| B、2,3,4 |
| C、3,4,5 |
| D、4,5,6 |
 实数a、b、c在数轴上的位置如图所示,化简下列代数式的值
实数a、b、c在数轴上的位置如图所示,化简下列代数式的值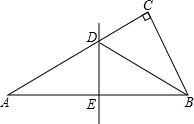 如图,△ABC中,∠ACB=90°,AB的垂直平分线交AC于点D,E为垂足.∠ABD:∠DBC=3:2,求∠A的度数.
如图,△ABC中,∠ACB=90°,AB的垂直平分线交AC于点D,E为垂足.∠ABD:∠DBC=3:2,求∠A的度数.