题目内容
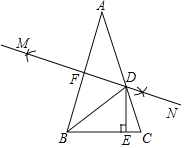
【题目】如图,在△ABC中,AB=AC,∠A=36°,分别以A和B为圆心,大于![]() AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
A.3B.2C.1D.0
【答案】A
【解析】
先根据等腰三角形的性质和三角形内角和得到∠ABC=∠C=72°,再利用基本作图得到MN垂直平分AB,则DA=DB,所以∠DBA=∠A=36°,于是可对①进行判断;接着根据角平分线的性质可对②进行判断;通过计算出∠BDC=72°得到∠BDC=∠C,则BC=BD=AD,所以BC+CD=AC=AB,然后利用AB=2AF可对③进行判断.
解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
由作法得MN垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=36°,
∴BD平分∠ABC,所以①正确;
∵DF⊥BF,DE⊥BE,
∴DE=DF,所以②正确;
∵∠BDC=∠A+∠ABD=36°+36°=72°,
∴∠BDC=∠C,
∴BC=BD=AD,
∴BC+CD=AC=AB,
∵MN垂直平分AB
∴AB=2AF,
∴BC+CD=2AF,所以③正确.
故选:A.

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 |
|
|
(1)完成上表;
(2)若从盒子中随机摸出一个球,则摸到白球的概率P= ;(结果保留小数点后一位)
(3)估算这个不透明的盒子里白球有多少个?