题目内容
【题目】请参照下面探究过程,完成所提出的问题.
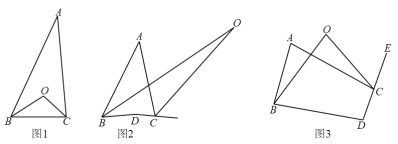
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点.
若∠A=30°,则∠BOC= ;
若∠A=α,则∠BOC= (用含α的代数式表示)
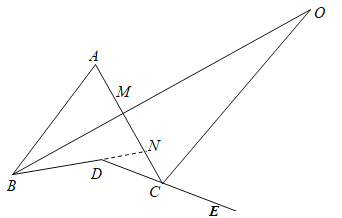
(2)如图2,在四边形ABDC中,点O是∠ABD和∠ACD外角平分线的交点,写出∠A、∠D与∠O之间的数量关系,并说明理由;
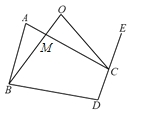
(3) 如图3,在四边形ABDC中,∠ABD和∠ACD外角的n等分线交于O,使∠ABD=n∠ABO,∠ACE=n∠ACO.直接写出∠A、∠D和∠O之间的数量关系.
【答案】(1)105°,90°+![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由三角形内角和定理可求得∠ABC+∠ACB,根据角平分线的定义可求得∠OBC+∠,在△BOC中利用三角形内角和定理可求得∠BOC;
(2)设AC与BO的交点为M,延长BD交AC于N,根据三角形内角和等于180°,四边形内角和等于360°,结合角平分线的定义即可得到∠A、∠D与∠O之间的数量关系;
(3)设AC与BO的交点为M,根据三角形内角和等于180°,四边形内角和等于360°,可得到![]() ,
,![]() ,将前式代入即可得到结论.
,将前式代入即可得到结论.
(1)∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵BO、CO是角平分线,
∴∠ABC=2∠OBC,∠ACB=2∠BCO,
∴∠OBC+∠BCO=75°,
∵∠OBC+∠BCO+∠BOC=180°,
∴∠BOC=105°;
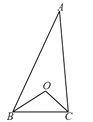
如图,在![]() 中,
中,![]() 是
是![]() 与
与![]() 的平分线
的平分线![]() 和
和![]() 的交点,
的交点,
![]()
![]()
![]()
(2)设AC与BO的交点为M,延长BD交AC于N,如图所示:
∵∠A+∠ABM+∠AMB=180°,
∴∠AMB=180°-∠A-∠ABM
∵BM是∠ABD的平分线,
∴∠ABM=![]() ∠ABD,
∠ABD,
∴∠AMB=180°-∠A-![]() ∠ABD
∠ABD
∵∠AMB=∠CMO,
∴∠CMO=180°-∠A-![]() ∠ABD,
∠ABD,
∵![]()
∴![]()
=![]()
=![]()
∴![]()
∵∠DNC是△ABN的外角,
∴∠DNC=∠A+∠ABN,
∵∠ACD与∠ACE互为邻补角,
∴∠ACD=180°-∠ACE,
∵∠BDC是△DCN的外角,
∴![]()
=![]()
=![]()
=![]()
![]()
(3)设AC与BO的交点为M,如图所示:
∵∠A+∠ABM+∠AMB=180°,
∴∠AMB=180°-∠A-∠ABM
∵∠AMB=∠CMO,
∴∠CMO=180°-∠A-∠ABM,
∵![]()
∴![]()
=![]()
=![]()
∴![]()
∵![]()
∴![]()
∵∠ACD+∠ACE=180°
∴∠ACD=180°-∠ACE
∵∠ABD=n∠ABO,∠ACE=n∠ACO,
∴∠D=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
![]()

 阅读快车系列答案
阅读快车系列答案【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?