题目内容
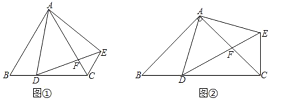
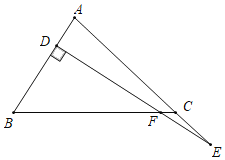
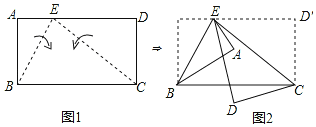
【题目】图1的矩形ABCD中，E点在AD上，且AB＝
，AE＝1．今分别以BE、CE为折线，将A、D向BC的方向折过去，图2为对折后A、B、C、D、E五点均在同一平面上的位置图．若图2中，∠AED＝15°，则∠AEC的度数是（ ）
A.10°B.15°C.20°D.22.5°
【答案】D
【解析】
由根据直角三角形30°角所对的直角边等于斜边的一半求出∠ABE＝30°，再根据直角三角形两锐角互余求出∠AEB＝60°，然后求出∠BED的度数，再根据平角等于180°求出∠DED′，然后根据翻折变换的性质求出∠CED，于是得到结论．
解：在长方形ABCD中，∠A＝90°，AD∥BC，
∵BE＝2AE，
∴∠ABE＝30°，
∴∠AEB＝90°﹣∠ABE＝90°﹣30°＝60°，
∵∠AED＝15°，
∴∠BED＝∠AEB﹣∠AED＝60°﹣15°＝45°，
∴∠DED′＝180°﹣60°﹣45°＝75°，
根据翻折的性质，∠CED′＝
∠DED′＝×75°＝37.5°，
∴∠AEC＝∠CED﹣∠AED＝22.5°．
故选：D．
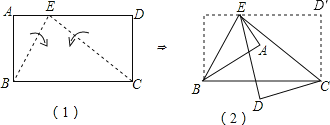
练习册系列答案
阅读快车系列答案
相关题目
