题目内容
在第一象限内,以
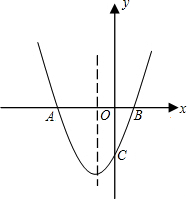
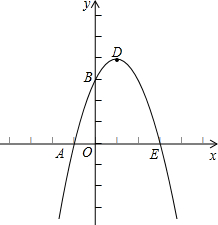
为半径的圆⊙M经过点A(-1,0),B(3,0),与y轴相交于点C.
(1)在所给的坐标系中作出⊙M,并求M点的坐标;
(2)求经过A、B、C三点的抛物线的解析式;
(3)若D为⊙M上的最低点,E为x轴上的任一点,则在抛物线上是否存在这样的点F,使得以点A、D、E、F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,说出理由.
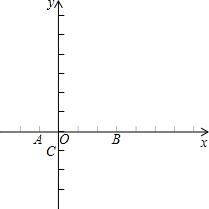
| 5 |
(1)在所给的坐标系中作出⊙M,并求M点的坐标;
(2)求经过A、B、C三点的抛物线的解析式;
(3)若D为⊙M上的最低点,E为x轴上的任一点,则在抛物线上是否存在这样的点F,使得以点A、D、E、F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,说出理由.
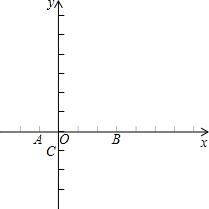
(1)∵A(-1,0),B(3,0),
∴AB=3-(-1)=3+1=4,
作AB的垂直平分线交AB于N,则AN=
AB=
×4=2,
∴ON=AN-AO=2-1=1,
根据勾股定理,MN=
=
=1,
∴点M的坐标为(1,1),
取MN=1,以点M为圆心,以AM长为半径作⊙M如图所示;
(2)设点C的坐标为(0,y),
则MC=
=
,
解得y1=-1,y2=3,
由图可知,点C在y轴负半轴,
∴点C的坐标为(-1,0),
设抛物线解析式为y=ax2+bx+c(a≠0),
则
,
解得
,
所以,抛物线解析式为y=
x2-
x-1;
(3)∵D为⊙M上的最低点,
∴点D的坐标为(1,1-
),
∵E为x轴上的任一点,以点A、D、E、F为顶点的四边形是平行四边形,
∴AE∥DF,
①点F在x轴下方,点F的纵坐标与点D的纵坐标相同,为1-
,
∵点F在抛物线上,
∴
x2-
x-1=1-
,
整理得,x2-2x-6+3
=0,
△=b2-4ac=4-4(-6+3
)=28-12
,
∴x=
=1±
,
∴点F的坐标为F1(1+
,1-
),F2(1-
,1-
),
此时可以分别以AD为平行四边形的边和对角线作一个平行四边形,共有4个平行四边形,
②点F在x轴上方时,点F的纵坐标与点的纵坐标的长度相同,为
-1,
∵点F在抛物线上,
∴
x2-
x-1=
-1,
整理得,x2-2x-3
=0,
△=b2-4ac=4-4×(-3
)=4+12
,
∴x=
=1±
,
∴点F的坐标分别为F3(1+
,
-1),F4(1-
,
-1),
此时,以AD为平行四边形的边共可以作2个平行四边形,
综上所述,共有6个符合条件的平行四边形,满足条件的F点有4个,分别是:
F1(1+
,1-
),F2(1-
,1-
),F3(1+
,
∴AB=3-(-1)=3+1=4,
作AB的垂直平分线交AB于N,则AN=
| 1 |
| 2 |
| 1 |
| 2 |
∴ON=AN-AO=2-1=1,
根据勾股定理,MN=
| AM2-AN2 |
|
∴点M的坐标为(1,1),
取MN=1,以点M为圆心,以AM长为半径作⊙M如图所示;
(2)设点C的坐标为(0,y),
则MC=
| (1-0)2+(1-y)2 |
| 5 |
解得y1=-1,y2=3,
由图可知,点C在y轴负半轴,
∴点C的坐标为(-1,0),
设抛物线解析式为y=ax2+bx+c(a≠0),
则
|
解得
|
所以,抛物线解析式为y=
| 1 |
| 3 |
| 2 |
| 3 |
(3)∵D为⊙M上的最低点,
∴点D的坐标为(1,1-
| 5 |
∵E为x轴上的任一点,以点A、D、E、F为顶点的四边形是平行四边形,
∴AE∥DF,
①点F在x轴下方,点F的纵坐标与点D的纵坐标相同,为1-
| 5 |
∵点F在抛物线上,
∴
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
整理得,x2-2x-6+3
| 5 |
△=b2-4ac=4-4(-6+3
| 5 |
| 5 |
∴x=
2±
| ||||
| 2×1 |
7-3
|
∴点F的坐标为F1(1+
7-3
|
| 5 |
7-3
|
| 5 |
此时可以分别以AD为平行四边形的边和对角线作一个平行四边形,共有4个平行四边形,
②点F在x轴上方时,点F的纵坐标与点的纵坐标的长度相同,为
| 5 |
∵点F在抛物线上,
∴
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
整理得,x2-2x-3
| 5 |
△=b2-4ac=4-4×(-3
| 5 |
| 5 |
∴x=
2±
| ||||
| 2 |
1+3
|
∴点F的坐标分别为F3(1+
1+3
|
| 5 |
1+3
|
| 5 |
此时,以AD为平行四边形的边共可以作2个平行四边形,
综上所述,共有6个符合条件的平行四边形,满足条件的F点有4个,分别是:
F1(1+
7-3
|
| 5 |
7-3
|
| 5 |
1+3
|

练习册系列答案
 名校课堂系列答案 名校课堂系列答案
相关题目
|


 点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______.
点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______.