题目内容
【题目】已知，二次函数
的图像经过点
（1）求此函数的解析式，并写出其顶点坐标；
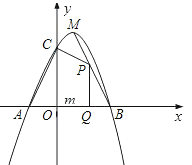
（2）在线段
上是否存在点
(不含
两点)，使
与
相似？若存在，请求出点的坐标；若不存在，请说明理由
【答案】（1）
，顶点为(1，4)；（2）存在，点P的坐标为(
)
【解析】
（1）已知了抛物线图象上三点的坐标，即可用待定系数法求出抛物线的解析式；用配方法将抛物线解析式化为顶点式，然后求出其顶点坐标；
（2）可分两种情况：
①△ABP∽△ABC，此时AB:AB=AP:AC，P、C重合，此种情况不合题意；
②△ABP∽△ACB，得AB:AC=AP:AB，由此可求出AP的长；易求得直线AC的解析式，可根据直线AC的解析式设出P点的坐标，再由AP的长求出P点的坐标．
（1）由题意得：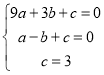
，
解得：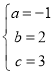
，
∴此函数解析式为
，
∵
，
∴顶点为(1，4)；
（2）假设存在点P，使△ABP与△ABC相似，
①△ABP∽△ABC，此时AB:AB=AP:AC，
∴AP=AC，即P、C重合，此种情况不合题意；
②△ABP∽△ACB，得AB:AC=AP:AB，
∵
，
∴
，
，
∴
直线AC的解析式为：
，
则
，
解得：
，
∴直线AC的解析式为：
，
设P
，其中
，
∴
解得：
(舍去)．
∴点P的坐标为(
) ．
练习册系列答案
相关题目
