题目内容
【题目】在△ABC中，∠BAC=90°,AB=AC,点D在BC边上，把△ABD沿AD折叠后，使得点B落在点E处，连接CE，若∠DBE=20°，则∠ADC=________.
【答案】70°或110°
【解析】分两种位置进行折叠，根据折叠的性质进行求解即可.
如图1，由折叠得，BD=DE，AB=AE，
∴∠DEB=∠DBE=20°
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,∠AED=45°
∴∠AEB=∠ABE=65°,
∴∠BAE=180°-65°-65°=50°,
∴∠EAD=∠BAD=
∠BAE=25°,
∴∠ADE=180°-25°-45°=110°,
∵∠CDE=20°+20°=40°
∴∠ADC=110°-40°=70°;
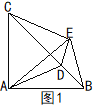
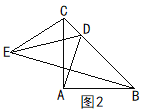
如图2，同理可得，∠ADC=110°.
故答案为：70°或110°.
练习册系列答案
相关题目
【题目】在东西向的马路上有一个巡岗亭
，巡岗员从岗亭出发以
速度匀速来回巡逻，如果规定向东巡逻为正，向西巡逻为负，巡逻情况记录如下：（单位：千米）
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
（1）第几次结束时巡逻员甲距离岗亭最远？距离有多远？
（2）甲巡逻过程中配置无线对讲机，并一直与留守在岗亭的乙进行通话，问甲巡逻过程中，甲与乙保持通话的时长共多少小时？
