题目内容
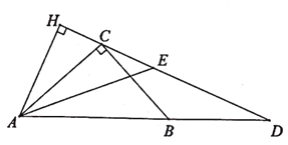
【题目】如衅,在Rt△ABC中,∠ACB=90°,sin∠BAC=![]() ,点D在AB的延长线上,BD=BC,AE平分∠BAC交CD于点E,若AE=5
,点D在AB的延长线上,BD=BC,AE平分∠BAC交CD于点E,若AE=5![]() ,则点A到直线CD的距离AH为________,BD的长为________.
,则点A到直线CD的距离AH为________,BD的长为________.
【答案】5; 2![]()
【解析】
证明HA=HE,理由等腰直角三角形的性质即可求出AH,由sin∠BAC=![]() ,设BC=BD=2k,AB=3k,则AC=
,设BC=BD=2k,AB=3k,则AC=![]() k,证明△HAC∽△HDA,可得AH2=HCHD,由△AHC∽△CMB,可得
k,证明△HAC∽△HDA,可得AH2=HCHD,由△AHC∽△CMB,可得![]() ,推出
,推出![]() ,推出CM=2
,推出CM=2![]() ,CD=4
,CD=4![]() ,可得25=HC(HC+4
,可得25=HC(HC+4![]() ),求出CH即可解决问题.
),求出CH即可解决问题.
如图,作BM⊥CD于M.

∵BC=BD,
∴∠D=∠BCD,
∵AH⊥DH,
∴∠H=∠ACB=90°,
∴∠ACH+∠HAC=90°,∠ACH+∠BCD=90°,
∴∠HAC=∠BCD=∠D,
∵AE平分∠CAB,
∴∠EAC=∠EAD,
∵∠HAE=∠HAC+∠EAC,∠AEH=∠D+∠EAD,
∴∠HAE=∠AEH,
∴HA=HE,
∵AE=5![]() ,
,
∴AH=HE=5,
∵sin∠BAC=![]() ,设BC=BD=2k,AB=3k,则AC=
,设BC=BD=2k,AB=3k,则AC=![]() k,
k,
∵∠H=∠H,∠HAC=∠D,
∴△HAC∽△HDA,
∴AH2=HCHD,
∵∠BCM=∠HAC,∠H=∠BMC=90°,
∴△AHC∽△CMB,
∴![]() ,
,
∴![]() ,
,
∴CM=2![]() ,
,
∵BC=BD,BM⊥CD,
∴CM=DM=2![]() ,
,
∴CD=4![]() ,
,
∴25=HC(HC+4![]() ),
),
∴HC=![]() 或-5
或-5![]() (舍弃),
(舍弃),
∴AC=![]() ,
,
∴![]() k=
k=![]() ,
,
∴k=![]() ,
,
∴BD=CB=2k=2![]() ,
,
故答案为5,2![]() .
.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案【题目】有这样一个问题:探究函数![]() 的图象与性质.小彤根据学习函数的经验,对函数
的图象与性质.小彤根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
x | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | ||
y |
|
|
|
|
| 0 |
|
| m |
|
|
(1)求m的值为 ;
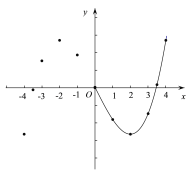
(2)如图,在平面直角坐标系x0y 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程![]() 实数根的个数为 ;
实数根的个数为 ;
(4)观察图象,写出该函数的一条性质 ;
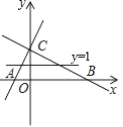
(5)在第(2)问的平面直角坐标系中画出直线![]() ,根据图象写出方程
,根据图象写出方程![]() 的一个正数根约为 (精确到0.1).
的一个正数根约为 (精确到0.1).