Question

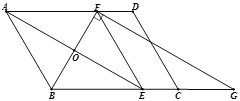
【题目】已知：如图，在四边形ABCD中，AB=CD，AD=BC，点E在CD上，连接AE并延长，交BC的延长线于F．

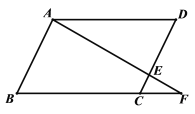
（1）求证：△ADE∽△FCE；

（2）若AB=4，AD=6，CF=2，求DE的长．

Answer 1

【答案】（1）见解析；（2）DE=3

【解析】

（1）根据已知条件得到四边形ABCD是平行四边形，根据AD∥BC证得∠DAE=∠F，∠D=∠DCF即可得到结论；

（2）根据（1）的△ADE∽△FCE列式即可求出答案.

（1）证明：∵ 四边形ABCD中，AB=CD，AD=BC，

∴ 四边形ABCD是平行四边形．

∴ AD∥BC．

∴ ∠DAE=∠F，∠D=∠DCF．

∴ △ADE∽△FCE．

（2）解：∵四边形ABCD是平行四边形，且AB=4，

∴AB=CD=4．

又∵△ADE∽△FCE，

∴

∵AD=6，CF=2，

∴

∴DE=3．