题目内容
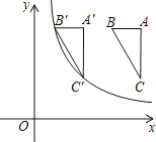
【题目】如图，在平面直角坐标系中，Rt△ABC的顶点B、C的坐标分别为(3，4)、(4，2)，且AB平行于x轴，将Rt△ABC向左平移，得到Rt△A′B′C′．若点B′、C′同时落在函数y=
（x＞0）的图象上，则k的值为（ ）
A.2B.4C.6D.8
【答案】B
【解析】
设平移的距离为m，由点B、C的坐标可以表示出B′、C′的坐标，B′、C′都在反比例函数的图象上，可得方程，求出m的值，进而确定点B′、C′的坐标，代入可求出k的值．
设Rt△ABC向左平移m个单位得到Rt△A′B′C′．
由B（3，4）、C（4，2），得：B′（3-m，4），C′（4-m，2）
点B′（3-m，4），C′（4-m，2）都在反比例函数的图象上，
∴（3-m）×4=（4-m）×2，
解得：m=2，
∴B′（1，4），C′（2，2）代入反比例函数的关系式得：k=4，
故选：B．
练习册系列答案
名题金卷系列答案
相关题目
