题目内容
【题目】如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9.
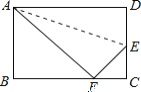
求:(1)FC的长;(2)EF的长.
【答案】(1)FC=3;(2)EF的长为5.
【解析】
(1)由折叠性质可得AF=AD,由勾股定理可求出BF的值,再由FC=BC-BF求解即可;
(2)由题意得EF=DE,设DE的长为x,则EC的长为(9-x)cm,在Rt△EFC中,由勾股定理即可求得EF的值.
解:(1)∵矩形对边相等,
∴AD=BC=15
∵折叠长方形的一边AD,点D落在BC边上的点F处
∴AF=AD=15,
在Rt△ABF中,由勾股定理得,![]()
∴FC=BC·BF=15-12=3
(2)折叠长方形的一边AD,点D落在BC边上的点F处
∴EF=DE
设DE=x,则EC=9·x,
在Rt△EFC中,由勾股定理得,![]()
即![]()
解得x=5
即EF的长为5。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
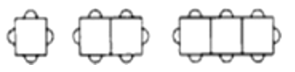
小学生10分钟应用题系列答案【题目】按下图方式摆放餐桌和椅子,
 …
…
(1)1张长方形餐桌可坐4人,2张长方形餐桌拼在一起可坐______人.
(2)按照上图的方式继续排列餐桌,完成下表.
桌子张数 | 3 | 4 | 5 | n |
可坐人数 | ______ | ______ | ______ | ______ |
(3)一家餐厅有40张这样的长方形餐桌,某用餐单位要求餐厅按照上图方式,每8张长方形餐桌拼成1张大桌子,则该餐厅此时能容纳多少人用餐?
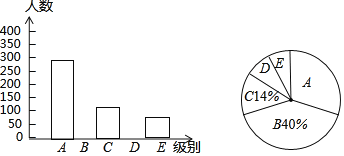
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.
组别 | 获取新闻的最主要途径 | 人数 |
A | 电脑上网 | 280 |
B | 手机上网 | m |
C | 电视 | 140 |
D | 报纸 | n |
E | 其它 | 80 |
请根据图表信息解答下列问题:
(1)统计表中的m= ,n= ,并请补全条形统计图;
(2)扇形统计图中“D”所对应的圆心角的度数是 ;
(3)若该市约有120万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.