题目内容
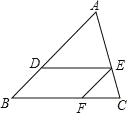
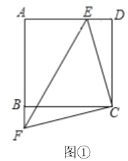
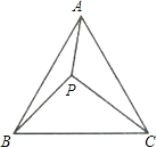
【题目】如图，点P为等边△ABC内一点，且PA=2 ，PB=1，,PC=
，求∠APB的度数.
【答案】120°
【解析】
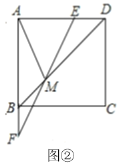
将△APC绕点A顺时针旋转60°得△ADB，首先证明△ADP为等边三角形得∠APD=60°、DP=AP=2、∠DPA=60°；其次证明DB2+BP2=DP2得到∠DBP=90°、∠DPB=60°，由∠APB=∠DPB+∠DPA即可解决问题．
∵△ABC为等边三角形，
∴AB=AC，∠BAC=60°，
将△APC绕点A顺时针旋转60°得△ADB，
∴AD=AP=2，DB=PC=
，∠DAP=60°，
∴△ADP为等边三角形，
∴DP=AP=2，∠DPA=60°，
在△DPB中，∵DB=、BP=1、DP=2，
∴DB2+BP2=DP2，
∴∠DBP=90°，∠DPB=60°，
∴∠APB=∠DPB+∠DPA=60°+60°=120°．
能力评价系列答案
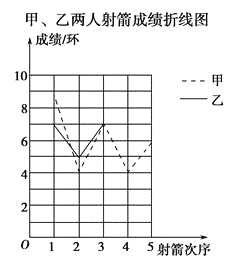
唐印文化课时测评系列答案
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩(单位：环)相同，小宇根据他们的成绩绘制了尚不完整的统计图表，并计算了甲成绩的平均数和方差(见小宇的作业)．
小宇的作业：
解：
甲＝
(9＋4＋7＋4＋6)＝6，
s甲2＝[(9－6)2＋(4－6)2＋(7－6)2＋(4－6)2＋(6－6)2]
＝(9＋4＋1＋4＋0)
＝3.6
小宇的作业：
解：甲＝(9＋4＋7＋4＋6)＝6，
s甲2＝[(9－6)2＋(4－6)2＋(7－6)2＋(4－6)2＋(6－6)2]
＝(9＋4＋1＋4＋0)
＝3.6
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a＝________，乙＝________；
(2)请完成图中表示乙成绩变化情况的折线；
(3)①观察图，可看出________的成绩比较稳定(填“甲”或“乙”)．参照小宇的计算方法，计算乙成绩的方差，并验证你的判断．
②请你从平均数和方差的角度分析，谁将被选中．
