题目内容
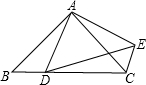
如图,D为等腰直角△ABC斜边BC上的一个动点(D与B、C均不重合),连接AD,以AD 为一边作等腰直角△ADE,DE为斜边,连接CE.
为一边作等腰直角△ADE,DE为斜边,连接CE.
(1)求证:△ACE≌△ABD;
(2)设BD=x,若AB= ;
;
①当△DCE的面积为1.5时,求x的值;
②试问:△DCE的面积是否存在最大值?若存在,请求出这个最大值,并指出此时x的取值;若不存在,请说明理由.
证明:(1)∵BC、DE分别是两个等腰直角△ADE、△ABC的斜边,
∴∠DAE=∠BAC=90°,
∴∠DAE-∠DAC=∠BAC-∠DAC=90°,
∴∠CAE=∠BAD.
在△ACE和△ABD中,
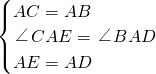
∴△ACE≌△ABD(SAS).
解:(2)①∵AC=AB= ,
,
∴BC 2=AC2+AB2=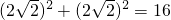 ,
,
∴BC=4.
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,同理∠ACE=45°,
∴∠DCE=90度.
∵△ACE≌△ABD,
∴CE=BD=x,而BC=4,
∴DC=4-x,
∴Rt△DCE的面积为 DC•CE=
DC•CE= (4-x)x.
(4-x)x.
∴ (4-x)x=1.5
(4-x)x=1.5
即x2-4x+3=0.
解得x=1或x=3.
②△DCE存在最大值,理由如下:
设△DCE的面积为y,于是得y与x的函数关系式为:
y= (4-x)x(0<x<4)
(4-x)x(0<x<4)
=- (x-2)2+2
(x-2)2+2
∵a=- <0,∴当x=2时,函数y有最大值2.
<0,∴当x=2时,函数y有最大值2.
又∵x满足关系式0<x<4,
故当x=2时,△DCE的最大面积为2.
分析:(1)△ACE可看作由△ABD绕点A逆时针旋转90°得到的,可由已知找全等的条件.
(2)由(1)可推出BD=CE,∠DCE=90°在Rt△CDE中,CD=4-x,CE=x,可表示△CDE的面积,用一元二次方程,二次函数解答本题.
点评:本题结合等腰直角三角形中的旋转观察全等三角形,考查了全等三角形的判定与性质的运用,通过计算面积又把问题与一元二次方程、二次函数进行综合应用.
∴∠DAE=∠BAC=90°,
∴∠DAE-∠DAC=∠BAC-∠DAC=90°,
∴∠CAE=∠BAD.
在△ACE和△ABD中,
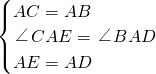
∴△ACE≌△ABD(SAS).
解:(2)①∵AC=AB=
 ,
,∴BC 2=AC2+AB2=
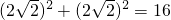 ,
,∴BC=4.
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,同理∠ACE=45°,
∴∠DCE=90度.
∵△ACE≌△ABD,
∴CE=BD=x,而BC=4,
∴DC=4-x,
∴Rt△DCE的面积为
 DC•CE=
DC•CE= (4-x)x.
(4-x)x.∴
 (4-x)x=1.5
(4-x)x=1.5即x2-4x+3=0.
解得x=1或x=3.
②△DCE存在最大值,理由如下:
设△DCE的面积为y,于是得y与x的函数关系式为:
y=
 (4-x)x(0<x<4)
(4-x)x(0<x<4)=-
 (x-2)2+2
(x-2)2+2∵a=-
 <0,∴当x=2时,函数y有最大值2.
<0,∴当x=2时,函数y有最大值2.又∵x满足关系式0<x<4,
故当x=2时,△DCE的最大面积为2.
分析:(1)△ACE可看作由△ABD绕点A逆时针旋转90°得到的,可由已知找全等的条件.
(2)由(1)可推出BD=CE,∠DCE=90°在Rt△CDE中,CD=4-x,CE=x,可表示△CDE的面积,用一元二次方程,二次函数解答本题.
点评:本题结合等腰直角三角形中的旋转观察全等三角形,考查了全等三角形的判定与性质的运用,通过计算面积又把问题与一元二次方程、二次函数进行综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
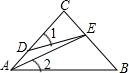 如图,△ABC为等腰直角三角形,若AD=
如图,△ABC为等腰直角三角形,若AD=| 1 |
| 3 |
| 1 |
| 3 |
| A、∠1>∠2 | B、∠1<∠2 |
| C、∠1=∠2 | D、无法确定 |
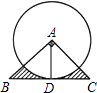 如图,△ABC为等腰直角三角形,∠A=90°,AB=AC=
如图,△ABC为等腰直角三角形,∠A=90°,AB=AC=| 2 |
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、1-
|
 如图,D为等腰直角三角形斜边BC上的一点,△ABD绕点A旋转后与△ACE重合,如果AD=1,那么DE=
如图,D为等腰直角三角形斜边BC上的一点,△ABD绕点A旋转后与△ACE重合,如果AD=1,那么DE= (2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( )
(2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( )