题目内容
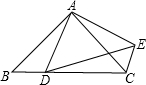 如图,D为等腰直角三角形斜边BC上的一点,△ABD绕点A旋转后与△ACE重合,如果AD=1,那么DE=
如图,D为等腰直角三角形斜边BC上的一点,△ABD绕点A旋转后与△ACE重合,如果AD=1,那么DE=分析:根据题意,△ABC是等腰直角三角形,△ABD≌△ACE,AD=1,故AD=AE=1,利用勾股定理可求出DE.
解答:解:因为△ABD与△ACE是互相旋转可得的,
故△ABD≌△ACE.
因为AD=1,
故AD=AE=1,
又可证△ADE是等腰直角三角形,
所以DE=
=
.
故△ABD≌△ACE.
因为AD=1,
故AD=AE=1,
又可证△ADE是等腰直角三角形,
所以DE=
| AD2+AE2 |
| 2 |
点评:本题难度较简单,主要考查的是旋转的性质以及勾股定理的相关知识.

练习册系列答案
相关题目
 抛物线的对称轴为直线x=m.求当k为何值时,|m|=
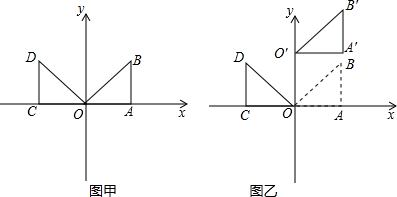
抛物线的对称轴为直线x=m.求当k为何值时,|m|= 所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD.
所示的等腰直角三角形BCD,点E在过A、C、D三点的圆上,且DE⊥BD,连结CE、AD. 为等腰直角三角形
为等腰直角三角形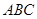 的重心,
的重心, ,直线
,直线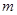 过点
过点 三点分别作直线
三点分别作直线 .
. 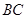 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段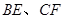 和
和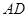 三者之间的数量关系并证明;
三者之间的数量关系并证明; 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.
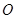 为等腰直角三角形
为等腰直角三角形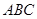 的重心,
的重心,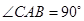 ,直线
,直线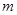 过点
过点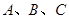 三点分别作直线
三点分别作直线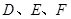 .
. 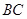 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段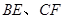 和
和 三者之间的数量关系并证明;
三者之间的数量关系并证明; 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.
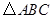 和的
和的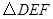 是等腰直角三形,
是等腰直角三形,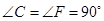 ,
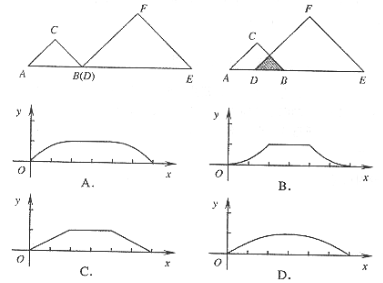
,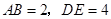 .点B与点D重合,点
.点B与点D重合,点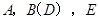 在同一条直线上,将
在同一条直线上,将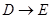 方向平移,至点
方向平移,至点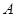 与点
与点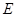 重合时停止.设点
重合时停止.设点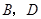 之间的距离为x,
之间的距离为x,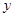 ,则准确反映
,则准确反映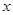 之间对应关系的图象是( )
之间对应关系的图象是( )