题目内容
如图,△ABC为等腰直角三角形,D为AB的中点,AB=2,扇形ADG、BDH的圆心角∠DAG、∠DBH都等于90度.求阴影部分图形的面积.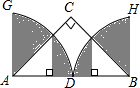
分析:由等腰直角三角形的性质知,点D是AB的中点,△AEF与△WSB是全等三角形,且为等腰直角三角形,则阴影部分的面积等于两个扇形的面积减去这两个小等腰直角三角形的面积.
解答: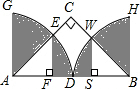
解:∵△ABC为等腰直角三角形,D为AB的中点,AB=2,
∴AD=BD=AE=WB=1,∠CAB=∠CBA=45°,
∵EF⊥AB,WS⊥AB,
∴△AEF与△WSB都是等腰直角三角形,有△AEF≌△WSB,AF=EF=WS=BS=AEsin45°=
S扇形AGD=S扇形BDH=
π•AD2=
π,
S△AEF=S△WSB=
AF2=
,
∴S阴影=2•S扇形AGD-2•S△AEF=
-
.

解:∵△ABC为等腰直角三角形,D为AB的中点,AB=2,
∴AD=BD=AE=WB=1,∠CAB=∠CBA=45°,
∵EF⊥AB,WS⊥AB,
∴△AEF与△WSB都是等腰直角三角形,有△AEF≌△WSB,AF=EF=WS=BS=AEsin45°=
| ||
| 2 |
S扇形AGD=S扇形BDH=
| 1 |
| 4 |
| 1 |
| 4 |
S△AEF=S△WSB=
| 1 |
| 2 |
| 1 |
| 4 |
∴S阴影=2•S扇形AGD-2•S△AEF=
| π |
| 2 |
| 1 |
| 2 |
点评:本题利用了等腰直角三角形的性质,等腰直角三角形的面积公式,圆的面积公式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
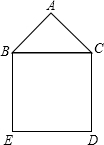 如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.
如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.| A、16 | B、24 | C、64 | D、32 |
 2、如图,△ABC为等腰三角形,AB=AC,∠A=40°,D,E,F分别在BC,AC,AB上,且CE=CD,BD=BF,则∠EDF的度数为( )
2、如图,△ABC为等腰三角形,AB=AC,∠A=40°,D,E,F分别在BC,AC,AB上,且CE=CD,BD=BF,则∠EDF的度数为( ) 如图,△ABC为等腰直角三角形∠BAC=90°,AD是斜边BC上的中线,△ABD旋转到△ACE的位置.
如图,△ABC为等腰直角三角形∠BAC=90°,AD是斜边BC上的中线,△ABD旋转到△ACE的位置. (2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( )
(2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( ) 如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形ABDC为( )
如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形ABDC为( )