题目内容
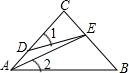 如图,△ABC为等腰直角三角形,若AD=
如图,△ABC为等腰直角三角形,若AD=| 1 |
| 3 |
| 1 |
| 3 |
| A、∠1>∠2 | B、∠1<∠2 |
| C、∠1=∠2 | D、无法确定 |
分析:先过E作EF⊥AB于F,设CA=CB=3,利用勾股定理求出EF=BF=
,再证明Rt△DCE与Rt△AFE相似即可得出答案.
| 2 |
解答: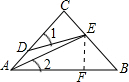 解:过E作EF⊥AB于F,设CA=CB=3,AB=3
解:过E作EF⊥AB于F,设CA=CB=3,AB=3
AD=
AC=1,CD=2
CE=
BC=1,EB=2
EF=BF=
AF=AB-BF=3
-
=2
,
所以
=
,
所以,Rt△DCE与Rt△AFE相似.
所以,∠1=∠2.
故选C.
 解:过E作EF⊥AB于F,设CA=CB=3,AB=3
解:过E作EF⊥AB于F,设CA=CB=3,AB=3| 2 |
AD=
| 1 |
| 3 |
CE=
| 1 |
| 3 |
EF=BF=
| 2 |
AF=AB-BF=3
| 2 |
| 2 |
| 2 |
所以
| CD |
| AF |
| CE |
| EF |
所以,Rt△DCE与Rt△AFE相似.
所以,∠1=∠2.
故选C.
点评:此题考查学生对等腰直角三角形,勾股定理和相似三角形的判定与性质的理解和掌握,此题的关键是过E作EF⊥AB,这是此题的突破点,然后利用相似三角形即可证明,此题属于中档题.

练习册系列答案
相关题目
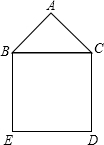 如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.
如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.| A、16 | B、24 | C、64 | D、32 |
 2、如图,△ABC为等腰三角形,AB=AC,∠A=40°,D,E,F分别在BC,AC,AB上,且CE=CD,BD=BF,则∠EDF的度数为( )
2、如图,△ABC为等腰三角形,AB=AC,∠A=40°,D,E,F分别在BC,AC,AB上,且CE=CD,BD=BF,则∠EDF的度数为( ) 如图,△ABC为等腰直角三角形∠BAC=90°,AD是斜边BC上的中线,△ABD旋转到△ACE的位置.
如图,△ABC为等腰直角三角形∠BAC=90°,AD是斜边BC上的中线,△ABD旋转到△ACE的位置. (2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( )
(2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( ) 如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形ABDC为( )
如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形ABDC为( )