题目内容
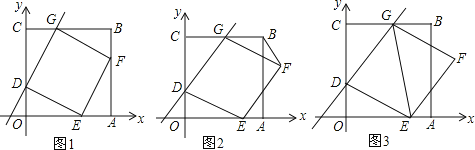
【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①![]() ;②
;②![]() .
.
(2)若![]() ,
,
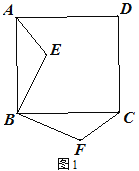
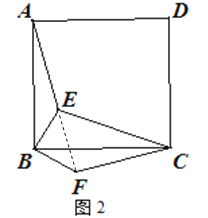
① 如图2,点E在正方形内,连接EC,若![]() ,
, ![]() ,求
,求![]() 的长;
的长;
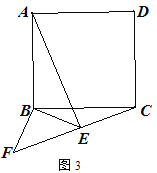
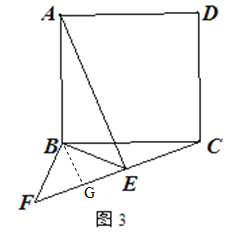
② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

【答案】见解析
【解析】试题分析:(1)①由旋转的性质得到△AEB≌△CFB,利用全等三角形的对应边对应角相等证明;
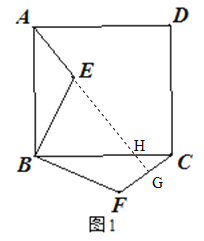
②延长AE交CF于G,交BC于H,证明∠HGC=∠ABC即可;
(2)①连接EF,由BE⊥BF且BE=BF,可得∠BFE=45°,EF2=8,这样在Rt△ECF中,
利用勾股定理可得FC的长, 即可得到结论;
②过点B作BG⊥FC于点G,利用勾股定理可得GC,GF的长,即可得到结论.
试题解析:解:(1)①由旋转的性质可知:△ABE≌△CBF,∴AE=CF;
②延长AE交CF于G,交BC于H.由旋转的性质可知:△ABE≌△CBF,∴∠BAE=∠BCF.∵∠AHB=∠CHG,∴∠HGC=∠ABC=90°,∴AE⊥CF;
(2)①连接EF.∵△ABE≌△CBF,∴∠ABE=∠CBF,BE=BF,∠BFC=∠BEA.∵∠ABC=90°,∴∠ABE+∠EBC=90°,∴∠EBC+∠FBC=90°,∴∠EBF=90°,∵BE=BF=2,∴EF2=22+22=8,∠BFE=45°,∴∠EFC=90°,∵EC=5,∴FC=![]() =
=![]() ,∴AE=
,∴AE=![]() ;
;
②过点B作BG⊥FC于点G.∵△FBE是等腰直角三角形,BE=2,∴BG=FG=GE=![]() ,在Rt△BGC中,GC=
,在Rt△BGC中,GC=![]() =
=![]() ,∴AE=CF=
,∴AE=CF=![]() .
.

练习册系列答案
相关题目