题目内容
【题目】已知函数f(x)= ![]() x2+ax2+bx﹣
x2+ax2+bx﹣ ![]() (a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|=
(a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|= ![]() ,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
(Ⅱ)证明关于x的方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根(其中f′(x)是f(x)的导函数,e是自然对数的底数)
【答案】解:(Ⅰ)求导f′(x)=x2+2ax+b,由f(x)在x=x1和x=x2处取得极值, 则x1 , x2是方程x2+2ax+b=0的两个根,则x1+x2=﹣2a,x1x2=b,
由|x1﹣x2|= ![]() ,则(x1+x2)2﹣4x1x2=5,则4a2﹣4b=5,①
,则(x1+x2)2﹣4x1x2=5,则4a2﹣4b=5,①
由曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直,
则f′(1)=1,
即2a+b+1=0,②,
解得: 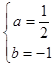 .
.
∴f(x)= ![]() x3+
x3+ ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,
,
(Ⅱ)对于(k2+1)ex﹣1﹣kf′(x)=0,
当k=0时,ex﹣1=0,方程为实根,
当k≠0时,k+ ![]() =
= ![]() ,令g(x)=
,令g(x)= ![]() ,
,
g′(x)=﹣e ![]() =﹣e
=﹣e ![]() ,
,
当x∈(﹣∞,﹣1)∪(2,+∞)时,g′(x)<0,
∴g(x)的单调递减区间(﹣∞,﹣1),(2,+∞)单调递增区间(﹣1,2),
函数g(x)在x=﹣1和x=2处分别求得极小值和极大值,
g(x)极小=g(﹣1)=﹣e2<0,g(x)极大=g(2)= ![]() >0,
>0,
∴对于g(x)= ![]() ,由ex﹣1>0恒成立,
,由ex﹣1>0恒成立,
且y=x2+x﹣1时与x轴有两个交点,
从而g(x)无极大值,g(x)min=g(x)极小=g(﹣1)=﹣e2 ,
当k<0时,k+ ![]() ≤﹣2直线y=k+
≤﹣2直线y=k+ ![]() ,与曲线y=g(x)至多有两个交点,
,与曲线y=g(x)至多有两个交点,
当k>0时,k+ ![]() ≥2>
≥2> ![]() =g(x)极大 , 直线y=k+
=g(x)极大 , 直线y=k+ ![]() ,与曲线y=g(x)只有一个交点,
,与曲线y=g(x)只有一个交点,
∴方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根.
【解析】(Ⅰ)由题意可知x1 , x2是方程x2+2ax+b=0的两个根,利用韦达定理及|x1﹣x2|= ![]() ,求得4a2﹣4b=5,由f′(1)=1,2a+b+1=0联立即可求得a和b的值,求得f(x)的解析式;(Ⅱ)由题意可知当k≠0时,k+
,求得4a2﹣4b=5,由f′(1)=1,2a+b+1=0联立即可求得a和b的值,求得f(x)的解析式;(Ⅱ)由题意可知当k≠0时,k+ ![]() =
= ![]() ,构造辅助函数,求导根据函数的单调性求得函数的极值及最值,利用基本不等式的性质,当k<0时,k+
,构造辅助函数,求导根据函数的单调性求得函数的极值及最值,利用基本不等式的性质,当k<0时,k+ ![]() ≤﹣2直线y=k+
≤﹣2直线y=k+ ![]() ,与曲线y=g(x)至多有两个交点,当k>0时,k+
,与曲线y=g(x)至多有两个交点,当k>0时,k+ ![]() ≥2>
≥2> ![]() =g(x)极大 , 直线y=k+
=g(x)极大 , 直线y=k+ ![]() ,与曲线y=g(x)只有一个交点,即可求证方程至多有两个实根.
,与曲线y=g(x)只有一个交点,即可求证方程至多有两个实根.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

 阅读快车系列答案
阅读快车系列答案【题目】某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 | 测试成绩(分) | 人数 |
优秀 | 45≤x≤50 | 140 |
良好 | 37.5≤x<45 | 36 |
及格 | 30≤x<37.5 | |
不及格 | x<30 | 6 |

根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有人,达到优秀的人数占本次测试总人数的百分比为%.
(2)本次测试的学生数为人,其中,体质健康成绩为及格的有人,不及格的人数占本次测试总人数的百分比为%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.