Question

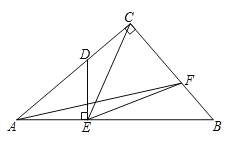
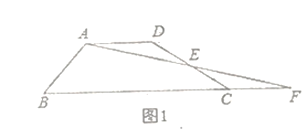
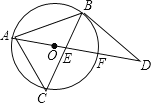
【题目】如图，点O为△ABC外接圆的圆心，以AB为腰作等腰△ABD，使底边AD经过点O，并分别交BC于点E、交⊙O于点F，若∠BAD＝30°．

（1）求证：BD是⊙O的切线；

（2）当CA2＝CECB时，

①求∠ABC的度数；

②的值．

Answer 1

【答案】（1）证明见解析；（2）①∠ABC＝45°；②＝．

【解析】

（1）由等腰三角形的性质可得∠D＝∠BAD＝30°＝∠ABO，由外角性质可得∠BOD＝60°，即可得∠OBD＝90°，可得结论；

（2）①由题意可证△ACE∽△BCA，可得∠CAE＝∠ABC＝∠CBF，由圆周角定理可求∠ABC的度数；

②通过证明△ACE∽△BFE，可得＝．

（1）连接OB，

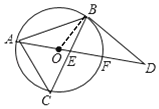
∵△ABD是等腰三角形，∠BAD＝30°

∴∠D＝∠BAD＝30°

∵OA＝OB

∴∠BAD＝∠ABO＝30°

∴∠BOD＝60°

∴∠OBD＝90°，

即OB⊥BD

∴BD是⊙O的切线；

（2）①连接BF

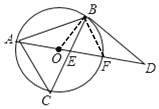
∵AF是直径

∴∠ABF＝90°

∵CA2＝CECB

∴且∠C＝∠C

∴△ACE∽△BCA

∴∠CAE＝∠ABC

∵∠CAE＝∠CBF

∴∠ABC＝∠CBF，且∠ABF＝90°

∴∠ABC＝45°

②连接OC

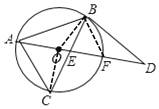
∵∠CAF＝∠ABC＝45°，AO＝CO

∴∠CAF＝∠ACO＝45°，∠AOC＝90°

∴AC＝OA

∵∠BOF＝60°，OF＝OB

∴△OBF是等边三角形

∴BF＝OF＝OB

∵∠CAF＝∠CBF，∠AFB＝∠ACB

∴△ACE∽△BFE

∴＝