题目内容
一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为【 】
| A.5 | B.5或6 | C.5或7 | D.5或6或7 |
D。
首先求得内角和为720°的多边形的边数,即可确定原多边形的边数
设内角和为720°的多边形的边数是n,则(n﹣2)•180=720,解得:n=6。
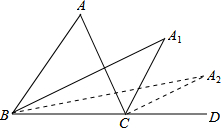
若截去一个角的多边形的直线经过两个顶点,则原多边形是七边形;
若截去一个角的多边形的直线经过一个顶点,则原多边形是六边形;
若截去一个角的多边形的直线不经过顶点,则原多边形是五边形。
∴原多边形的边数为5或6或7。故选D。
设内角和为720°的多边形的边数是n,则(n﹣2)•180=720,解得:n=6。
若截去一个角的多边形的直线经过两个顶点,则原多边形是七边形;
若截去一个角的多边形的直线经过一个顶点,则原多边形是六边形;
若截去一个角的多边形的直线不经过顶点,则原多边形是五边形。
∴原多边形的边数为5或6或7。故选D。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



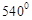 ,则这个多边形是【 】
,则这个多边形是【 】