Question

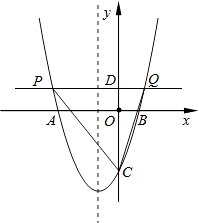
【题目】如图，在平面直角坐标系xOy中，二次函数y=ax2+bx﹣3（a，b是常数）的图象与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C．动直线y=t（t为常数）与抛物线交于不同的两点P、Q．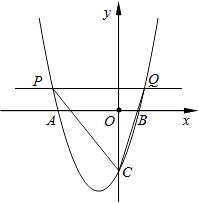

（1）求a和b的值；
（2）求t的取值范围；
（3）若∠PCQ=90°，求t的值．

Answer 1

【答案】
（1）

解：将点A、点B的坐标代入可得： ，

解得：

（2）

解：抛物线的解析式为y=x2+2x﹣3，直线y=t，

联立两解析式可得：x2+2x﹣3=t，即x2+2x﹣（3+t）=0，

∵动直线y=t（t为常数）与抛物线交于不同的两点，

∴△=4+4（3+t）＞0，

解得：t＞﹣4

（3）

解：∵y=x2+2x﹣3=（x+1）2﹣4，

∴抛物线的对称轴为直线x=﹣1，

当x=0时，y=﹣3，∴C（0，﹣3）．

设点Q的坐标为（m，t），则P（﹣2﹣m，t）．

如图，设PQ与y轴交于点D，则CD=t+3，DQ=m，DP=m+2．

∵∠PCQ=∠PCD+∠QCD=90°，∠DPC+∠PCD=90°，

∴∠QCD=∠DPC，又∠PDC=∠QDC=90°，

∴△QCD∽△CPD，

∴ ，即 ，

整理得：t2+6t+9=m2+2m，

∵Q（m，t）在抛物线上，∴t=m2+2m﹣3，∴m2+2m=t+3，

∴t2+6t+9=t+3，化简得：t2+5t+6=0

解得t=﹣2或t=﹣3，

当t=﹣3时，动直线y=t经过点C，故不合题意，舍去．

∴t=﹣2

【解析】（1）将点A、点B的坐标代入二次函数解析式可求出a、b的值；（2）根据二次函数及y=t，可得出方程，有两个交点，可得△＞0，求解t的范围即可；（3）证明△QCD∽△CPD，利用相似三角形的对应边成比例，可求出t的值．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．