Question

【题目】已知点D与点A（8，0），B（0，6），C（a，﹣a）是一平行四边形的四个顶点，则CD长的最小值为．

Answer 1

【答案】7
【解析】解：有两种情况： ①CD是平行四边形的一条边，那么有AB=CD= =10
②CD是平行四边形的一条对角线，
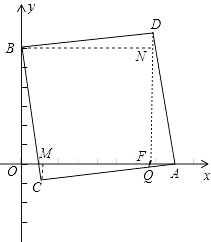
过C作CM⊥AO于M，过D作DF⊥AO于F，交AC于Q，过B作BN⊥DF于N，
则∠BND=∠DFA═∠CMA=∠QFA=90°，
∠CAM+∠FQA=90°，∠BDN+∠DBN=90°，
∵四边形ACBD是平行四边形，
∴BD=AC，∠C=∠D，BD∥AC，
∴∠BDF=∠FQA，
∴∠DBN=∠CAM，
∵在△DBN和△CAM中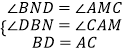

∴△DBN≌△CAM（AAS），
∴DN=CM=a，BN=AM=8﹣a，
D（（8﹣a，6+a），
由勾股定理得：CD2=（8﹣a﹣a）2+（6+a+a）2=8a2﹣8a+100=8（a﹣ ）2+98，
当a= 时，CD有最小值，是
∵ ＜10，
∴CD的最小值是 =7 ．
解法二：
CD是平行四边形的一条对角线
设CD、AB交于点E，
∵点E为AB的中点，
∴E（ ），即E（4，3）
∵CE=DE，
∴当DE取得最小值时，CE自然为最小，
∵C（a，﹣a），
∴C点可以看成在直线y=﹣x上的一点，
∴CE最小值为点E到直线的距离，即CE⊥直线y=﹣x，
根据两直线垂直，斜率乘积为﹣1，
∴CE所在直线为y=x+b，代入E（4，3），可得y=x﹣1，
∴C点坐标为两直线交点： ，即：（ ，﹣ ）
∴CE为： =
∴CD=7 ．
所以答案是：7 ．

【考点精析】利用平行四边形的性质对题目进行判断即可得到答案，需要熟知平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．