题目内容
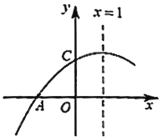
【题目】如图所示,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的一个根.其中正确的有( )
的一个根.其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
根据抛物线的开口方向、对称轴、与y轴交点的位置可得a、b、c的取值范围,由此可判断①;根据b=2a结合c的取值范围可对②进行判断;由OA=OC可得A的坐标,代入解析式可判断③;由点A坐标结合对称轴可得点B坐标,据此可判断④.
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=![]() =1,
=1,
∴b=2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵b=2a,
∴a+![]() b=aa=0,
b=aa=0,
∵c>0,
∴a+![]() b+
b+![]() c>0,所以②错误;
c>0,所以②错误;
∵C(0,c),OA=OC,
∴A(c,0),
把A(c,0)代入y=ax2+bx+c得ac2bc+c=0,
∴acb+1=0,所以③错误;
∵A(c,0),对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(2+c,0),
∴2+c是关于x的一元二次方程ax2+bx+c=0的一个根,所以④正确;
综上正确的有2个,
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】下表中给出![]() ,
,![]() ,
,![]() 三种手机通话的收费方式.
三种手机通话的收费方式.
收费方式 | 月通话费/元 | 包时通话时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
(1)设月通话时间为![]() 小时,则方案
小时,则方案![]() ,
,![]() ,
,![]() 的收费金额
的收费金额![]() ,
,![]() ,
,![]() 都是
都是![]() 的函数,请分别求出这三个函数解析式.
的函数,请分别求出这三个函数解析式.
(2)填空:
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
(3)小王、小张今年![]() 月份通话费均为
月份通话费均为![]() 元,但小王比小张通话时间长,求小王该月的通话时间.
元,但小王比小张通话时间长,求小王该月的通话时间.