题目内容
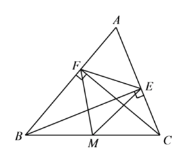
【题目】(8分)如图,AC是ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
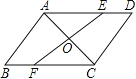
(1)求证:△AOE≌△COF;
(2)当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.
【答案】(1)参见解析;(2)EF⊥AC时,四边形AFCE是菱形.
【解析】
试题(1)由平行四边形的性质得出AD∥BC,得出∠EAO=∠FCO,利用对顶角相等∠AOE=∠COF,O是AC的中点,OA=OC,所以由ASA即可得出结论;(2)此题应用菱形的判定,先说明四边形AFCE已经是平行四边形,再应用对角线互相垂直的平行四边形是菱形即可.由△AOE≌△COF,得出对应边相等AE=CF,证出四边形AFCE是平行四边形,再由对角线EF⊥AC,即可得出四边形AFCE是菱形.
试题解析:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAO=∠FCO,∵O是CA的中点,∴OA=OC,又∵∠AOE=∠COF(对顶角相等),∴△AOE≌△COF(ASA);(2)∵△AOE≌△COF,∴AE=CF,∵AE∥CF,∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形),当EF⊥AC时四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形),∴EF⊥AC时,四边形AFCE是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目