题目内容
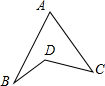如图所示，已知∠A=65°，∠B=20°，∠C=32°，则∠BDC的度数是
- A.135°
- B.128°
- C.117°
- D.97°
C
分析：连接AD并延长，根据三角形内角和外角的性质可得出∠3=∠1+∠B，∠4=∠2+∠C，再把两式相加即可．
解答：连接AD并延长，
∵∠3是△ABD的外角，∴∠3=∠1+∠B，
∵∠4是△ACD的外角，∴∠4=∠2+∠C，
两式相加得，∠3+∠4=∠1+∠B+∠2+∠C，即∠D=65°+20°+32°=117°．
故选C．
点评：本题考查的是三角形内角与外角的关系．解答此题的关键是作出辅助线，构造出三角形，再利用三角形内角与外角的关系解答．
分析：连接AD并延长，根据三角形内角和外角的性质可得出∠3=∠1+∠B，∠4=∠2+∠C，再把两式相加即可．
解答：连接AD并延长，
∵∠3是△ABD的外角，∴∠3=∠1+∠B，
∵∠4是△ACD的外角，∴∠4=∠2+∠C，
两式相加得，∠3+∠4=∠1+∠B+∠2+∠C，即∠D=65°+20°+32°=117°．
故选C．
点评：本题考查的是三角形内角与外角的关系．解答此题的关键是作出辅助线，构造出三角形，再利用三角形内角与外角的关系解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
52、如图所示，已知AB=AC，EB=EC，AE的延长线交BC于D，那么图中的全等三角形共有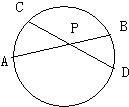
9、如图所示，已知⊙O中，弦AB，CD相交于点P，AP=6，BP=2，CP=4，则PD的长是（ ）
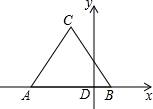如图所示，已知等边△ABC的两个顶点的坐标为A（-4，0），B（2，0）．
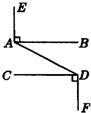24、如图所示，已知EA⊥AB于点A，CD⊥DF于点D，AB∥CD，请判断EA与DF的位置关系，并说明理由．
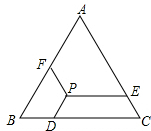如图所示，已知等边△ABC的边长为a，P是△ABC内一点，PD∥AB，PE∥BC，PF∥AC，点D、E、F分别在BC、AC、AB上，猜想：PD+PE+PF=