题目内容
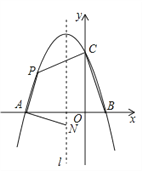
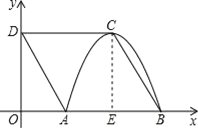
【题目】如图,四边形ABCD是菱形,点D的坐标是(0,![]() ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
(1)求A、B、C三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位长度.

【答案】(1)(1,0)、(3,0)、(2,![]() );(2)y=–
);(2)y=–![]() (x–2)2+
(x–2)2+![]() ;(3)向上平移了5
;(3)向上平移了5![]() –
–![]() =4
=4![]() 个单位长度
个单位长度
【解析】试题分析:(1)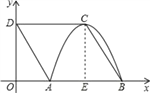
过C作CE⊥AB于E,根据抛物线的对称性知AE=BE;由于四边形ABCD是菱形,易证得△OAD≌△EBC,则OA=AE=BE,设OA=AE=BE=m,则菱形的边长为2m,在Rt△BCE中,根据勾股定理即可求出m的值,由此可确定A、B、C三点的坐标;
(2)根据(1)题求得的三点坐标,用待定系数法即可求出抛物线的解析式;
(3)设出平移后的抛物线解析式,将D点坐标代入此函数的解析式中,即可求出平移后的函数解析式,与原二次函数解析式进行比较即可得到平移的单位.
解:(1)过C作CE⊥AB于E,由抛物线的对称性可知AE=BE,
∵四边形ABCD是菱形,
∴CD//AB, AD=BC,
∴∠DCE=∠CEO=90°,
又∠DOA=90°, ∴四边形ODCE为矩形,
∴OD=CE,
在Rt△AOD和Rt△BEC中,
∵OD=EC,AD=BC,
∴Rt△AOD≌Rt△BEC(HL),
∴OA=BE=AE,
设OA=AE=BE=m,则菱形的边长为2m,
∵D(0,![]() ), ∴OD=CE=
), ∴OD=CE=![]() ,
,
在Rt△AOD中,![]() ,
,
∴ m2+(![]() )2=(2m)2,
)2=(2m)2,
解得m =1;
∴DC=2,OA=1,OB=3;
∴A、B、C三点的坐标分别为(1,0)、(3,0)、(2,![]() );
);
(2)由(1)知顶点C(2,![]() ),可设抛物线的解析式为y=a(x﹣2)2+
),可设抛物线的解析式为y=a(x﹣2)2+![]() ,
,
代入A点坐标可得![]() ,
,
解得a =﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ;
;
(3)设平移后的抛物线的解析式为 y=﹣![]() (x﹣2)2+k,
(x﹣2)2+k,
代入D(0,![]() )可得
)可得![]() ,
,
解得k=5![]() ,
,
所以平移后的抛物线的解析式为y=﹣![]() (x﹣2)2+5
(x﹣2)2+5![]() ,
,
向上平移了5![]() ﹣
﹣![]() =4
=4![]() 个单位.
个单位.