题目内容
【题目】如图所示,在四边形ABCD中,∠BAD=90°,AD=3cm,AB=4 cm,BC=5 cm, CD=6 cm.
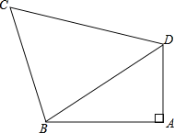
(1)连结BD,判断△CBD的形状;
(2)求四边形ABCD的面积S.
【答案】(1) △CBD是等腰三角形;(2) 18cm2.
【解析】
(1)求出BD的长,根据三边长判断三角形的形状;
(2)作BE⊥CD于E,求出BE的长,从而求得△BCD的面积,△ABD的面积很容易求出,进而可求得四边形ABCD的面积.
(1)∵∠BAD=90°,AD=3cm,AB=4cm,
∴BD=![]() =5cm,
=5cm,
∵BC=5cm,
∴BC=BD,
∴△CBD是等腰三角形.
(2)作BE⊥CD于E,
∵BC=BD,CD=6cm,
∴ DE=3cm,
∵BD=5cm,
∴BE=![]() =4cm,
=4cm,
∴S△CBD![]() =12cm2,
=12cm2,
∵S△ABD![]() =6cm2.
=6cm2.
故四边形ABCD的面积为12+6=18cm2.

练习册系列答案
相关题目
【题目】已知![]() 在数轴上分别表示
在数轴上分别表示![]() .
.
(1)对照数轴填写下表:
| 5 |
|
|
| 3 |
|
| 2 | 0 | 2 |
|
|
|
| 3 | 7 | ________ | 4 | ________ | 0 |
(2)若![]() 两点间的距离记为
两点间的距离记为![]() ,试问
,试问![]() 和
和![]() 有何数量关系?
有何数量关系?
(3)数轴上的整数点为![]() ,它到3和
,它到3和![]() 的距离之和为7,写出这些整数.
的距离之和为7,写出这些整数.
(4)若点![]() 表示的数为
表示的数为![]() ,当点
,当点![]() 在什么位置时,
在什么位置时,![]() 取得的值最小?
取得的值最小?