题目内容
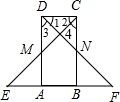
如图所示，在?ABCD中，AD=2AB，EA=AB=BF．求证：CE⊥DF．
证明：∵AD=2AB，AB=BF，
∴AD=AF，∠3=∠F．
∵四边形ABCD是平行四边形，
∴DC∥AB，AD∥BC．
∴∠1=∠F．
∴∠1=∠3．
同理，∠2=∠4．
∵∠1+∠2+∠3+∠4=180°．
∴∠1+∠2=90°．
∴CE⊥DF．
∴AD=AF，∠3=∠F．
∵四边形ABCD是平行四边形，
∴DC∥AB，AD∥BC．
∴∠1=∠F．
∴∠1=∠3．
同理，∠2=∠4．
∵∠1+∠2+∠3+∠4=180°．
∴∠1+∠2=90°．
∴CE⊥DF．
练习册系列答案
优学名师名题系列答案
相关题目
