题目内容
【题目】如图,已知直角坐标平面上的![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .若抛物线
.若抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.

![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 将抛物线向上平移若干个单位得到的新抛物线恰好经过点
将抛物线向上平移若干个单位得到的新抛物线恰好经过点![]() ,求新抛物线的解析式;
,求新抛物线的解析式;
![]() 设
设![]() 中的新抛物的顶点
中的新抛物的顶点![]() 点,
点,![]() 为新抛物线上
为新抛物线上![]() 点至
点至![]() 点之间的一点,以点
点之间的一点,以点![]() 为圆心画图,当
为圆心画图,当![]() 与
与![]() 轴和直线
轴和直线![]() 都相切时,联结
都相切时,联结![]() 、
、![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)新抛物线的解析式为
;(2)新抛物线的解析式为![]() ;(3)5
;(3)5
【解析】
(1)把A(-1,0)、C(3,0)代入![]() ,即可求得a、b的值;(2)设抛物线向上平移
,即可求得a、b的值;(2)设抛物线向上平移![]() 个单位后得到的新抛物线恰好经过点
个单位后得到的新抛物线恰好经过点![]() ,则新抛物线的解析式为
,则新抛物线的解析式为![]() ,再求得点
,再求得点![]() 的坐标为
的坐标为![]() .代入求得k值,即可求得新抛物线的解析式;(3)设⊙Q与x轴相切于点D,与直线BC相切于点E,连接QD、QE,易证四边形QECD是正方形,则有QD=DC.设点Q的横坐标为t,从而得到点Q的坐标为(t,3-t),代入新抛物线的解析式,求出点Q的坐标,然后运用割补法就可求出四边形ABQP的面积.
.代入求得k值,即可求得新抛物线的解析式;(3)设⊙Q与x轴相切于点D,与直线BC相切于点E,连接QD、QE,易证四边形QECD是正方形,则有QD=DC.设点Q的横坐标为t,从而得到点Q的坐标为(t,3-t),代入新抛物线的解析式,求出点Q的坐标,然后运用割补法就可求出四边形ABQP的面积.
![]() ∵抛物线
∵抛物线![]() 经过
经过![]() 、
、![]() ,
,
∴![]() ,
,
解得:![]() ;
;
![]() 设抛物线向上平移
设抛物线向上平移![]() 个单位后得到的新抛物线恰好经过点
个单位后得到的新抛物线恰好经过点![]() ,
,
则新抛物线的解析式为![]() ,
,
∵![]() 、
、![]() ,
,
∴![]() ,
,
∵![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ./p>
./p>
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
解得:![]() ,
,
∴新抛物线的解析式为![]() ;
;
![]() 设
设![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与直线
,与直线![]() 相切于点
相切于点![]() ,连接
,连接![]() 、
、![]() ,如图所示,
,如图所示,
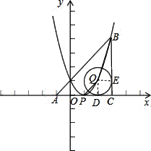
则有![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形.
是矩形.
∵![]() ,
,
∴矩形![]() 是正方形,
是正方形,
∴![]() .
.
设点![]() 的横坐标为
的横坐标为![]() ,
,
则有![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
解得:![]() ,
,![]() .
.
∵![]() 为抛物线
为抛物线![]() 上
上![]() 点至
点至![]() 点之间的一点,
点之间的一点,
∴![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() .
.
由![]() 得顶点
得顶点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
∴四边形![]() 的面积为
的面积为![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目