题目内容
如图，在直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数
图象交于A（-2，1）、B（1，n）两点．
（1）求上述反比例函数一次函数的表达式；
（2）观察图象，写出一次函数值小于反比例函数值的x的取值范围？
（3）连接AO、BO，求△AOB的面积．
解：（1）将A（-2，1）代入反比例解析式得：m=-2，则反比例解析式为y=-
；将B（1，n）代入反比例解析式得：n=-2，即B（1，-2），
将A与B坐标代入y=kx+b中，得：
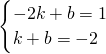，解得：
，则一次函数解析式为y=-x-1；
（2）由图象得：一次函数值小于反比例函数值的x的取值范围为-2＜x＜0或x＞1；
（3）连接OA，OB，设一次函数与x轴交于点C，
对于一次函数y=-x-1，令y=0，得到x=-1，即OC=1，
则S△AOB=S△AOC+S△BOC=
×1×1+×1×2=1.5．分析：（1）将A坐标代入反比例解析式求出m的值，确定出反比例解析式，将B坐标代入反比例解析式求n的值，确定出B坐标，将A与B坐标代入一次函数解析式求出k与b的值，即可确定出一次函数解析式；
（2）由A与B的横坐标，以及0，将x轴分为4个范围，找出反比例函数图象位于一次函数图象上方时x的范围即可；
（3）设一次函数与x轴交于C点，求出C坐标，确定出OC的长，三角形AOB面积=三角形AOC面积+三角形BOC面积，求出即可．
点评：此题考查了一次函数与反比例函数的交点问题，涉及的知识有：坐标与图形性质，待定系数法确定函数解析式，利用了数形结合的思想，熟练掌握待定系数法是解本题的关键．
练习册系列答案
相关题目
是方程x2-10x+16=0的两个根，且x1＜x2，连接MC，过A、B、C三点的抛物线的顶点为N．
半径的圆与抛物线是否还有除G点以外的交点？若有，请找出这个交点坐标．
已如：如图，在直角坐标系中，以y轴上的点C为圆心，2为半径的圆与x轴相切于原点O，AB为⊙C的直径，PA切⊙O于点A，交x轴的负半轴于点P，连接PC交OA于点D．
如图：在直角坐标系中描出A（-4，-4），B（1，-4），C（2，-1），D（-3，-1）四个点．