Question

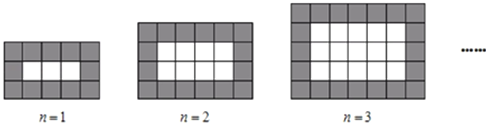
【题目】已知在矩形ABCD中，AB=2，AD=4．P是对角线BD上的一个动点（点P不与点B、D重合），过点P作PF⊥BD，交射线BC于点F．联结AP，画∠FPE=∠BAP，PE交BF于点E．设PD=x，EF=y．

（1）当点A、P、F在一条直线上时，求△ABF的面积；

（2）如图1，当点F在边BC上时，求y关于x的函数解析式，并写出函数定义域；

（3）联结PC，若∠FPC=∠BPE，请直接写出PD的长．

Answer 1

【答案】（1）1；（2）y=；（3）PD的长为±1或．

【解析】试题分析：（1）根据矩形ABCD ， A、P、F在一条直线上，且PF⊥BD，可得， ，得一，从而可得 ；

（2）先证明∽ ，从而得到 ，由AD//BC ，可得，从而根据三角函数可得 ，由得 ，代入，即可得；

（3）分∠CPF的∠FPE的内部与外部两种情况进行讨论即可得.

试题解析：（1）∵矩形ABCD ，∴，

∴ ， ∵A、P、F在一条直线上，且PF⊥BD，

∴ ， ∴，

∴，∵，

∴ ， ∴，

∴ ；

（2）∵PF⊥BP ，∴，

∴ ，∵ ，∴，

∴， 又∵∠BAP =∠FPE，

∴∽ ，∴ ，

∵AD//BC ， ∴，

∴ ， 即 ，

∵ ， ∴ ，

∴，

∴；

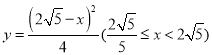（3）∠CPF=∠BPE，

①如图所示，当点F在CE上时，

∵∠BPF=∠FPD=90°，∴∠DPC=∠FPE，

∵∠FPE=∠BAP，∴∠DPC=∠BAP，

∵AB//CD，∴∠ABD=∠CDB，

∴△PAB∽△CPD，

∴PB：CD=AB：PD，

∴PB·PD=CD·AB，

∴x（）=2×2，

∴x=；

②如图所示，当点F在EC延长线上时，

过点P作PN⊥CD于点N，在CD上取一点M，连接PM，使∠MPF=∠CPF，

则有PC：PM=CH：MH，

∵∠BPF=∠DPF=90°，∴∠BPC=∠DPM，

∵∠BPE=∠CPF，∴∠BPE=∠EPF，

∵∠BAP=∠FPE，∴∠BAP=∠DPM，

∵∠ABD=∠BDC，

∴△PAB∽△MPD，

∴PB：MD=AB：PD，

由PD=x，tan∠PDM=tan∠PFC=2，

易得：DN= ，PN= ，CN=2- ，

PH=2x，FH= ，CH=2-x，

由PB：MD=AB：PD可得MD= ，从而可得MN，

在Rt△PCN中利用勾股定理可得PC，

由PC：PM=CH：MH可得PM，

在在Rt△PMN中利用勾股定理可得关于x 的方程，

解得x= ，

综上：PD的长为： 或 .