Question

【题目】已知：如图，在矩形ABCD中，AC是对角线，AB＝6cm，BC＝8cm．点P从点D出发，沿DC方向匀速运动，速度为1cm/s，同时，点Q从点C出发，沿CB方向匀速运动，速度为2cm/s，过点Q作QM∥AB交AC于点M，连接PM，设运动时间为t（s）（0＜t＜4）．解答下列问题：

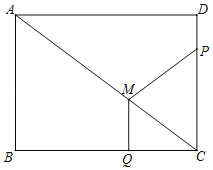
（1）当t为何值时，∠CPM＝90°；

（2）是否存在某一时刻t，使S四边形MQCP＝？若存在，求出t的值；若不存在，请说明理由；

（3）当t为何值时，点P在∠CAD的角平分线上．

Answer 1

【答案】（1）t＝s时，∠CPM＝90°；（2）t＝3s时，S四边形MQCP＝；（3）当t＝s时，点P在∠CAD的平分线上．

【解析】

（1）首先证明QM=PC，利用平行线分线段成比例定理构建方程即可解决问题．
（2）根据S四边形MQCP＝，构建方程即可解决问题．
（3）如图1中，作PH⊥AC于H．证明△PAD≌△PAH（AAS），推出AD=AH=8，DP=PH，设DP=PH=x，在Rt△PCH中，构建方程即可解决问题．

解：（1）∵四边形ABCD是矩形，

∴AB＝CD＝6，BC＝AD＝8，∠D＝90°，

∴AC＝＝10，

∵∠CPM＝∠D＝90°，

∴PM∥AD，

∵QM∥AB∥CD，

∴四边形PCQM是平行四边形，

∴PC＝QM＝6﹣t，

∵＝，

∴＝，

解得t＝，

∴t＝s时，∠CPM＝90°．

（2）∵S四边形MQCP＝，

∴（6﹣t）2t+2t×2t＝×6×8，

解得t＝3或﹣15（舍弃），

答：t＝3s时，S四边形MQCP＝．

（3）如图1中，作PH⊥AC于H．

∵∠D＝∠AHP＝90°，AP＝AP，∠PAD＝∠PAH，

∴△PAD≌△PAH（AAS），

∴AD＝AH＝8，DP＝PH，设DP＝PH＝x，

∵AC＝10，

∴CH＝2，

在Rt△PCH中，∵PH2+CH2＝PC2，

∴t2+22＝（6﹣t）2，

解得t＝，

答：当t＝s时，点P在∠CAD的平分线上．