题目内容
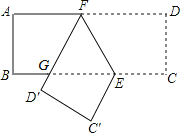
【题目】如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为______(用含t的代数式表示).
【答案】2![]() t
t
【解析】
根据翻折的性质可得CE=C′E,再根据直角三角形30°角所对的直角边等于斜边的一半判断出∠EBC′=30°,然后求出∠BGD′=60°,根据对顶角相等可得∠FGE=∠∠BGD′=60°,根据两直线平行,内错角相等可得∠AFG=∠FGE,再求出∠EFG=60°,然后判断出△EFG是等边三角形,根据等边三角形的性质表示出EF,即可得解.
解:由翻折的性质得,CE=C′E,

∵BE=2CE,
∴BE=2C′E,
又∵∠C′=∠C=90°,
∴∠EBC′=30°,
∵∠FD′C′=∠D=90°,
∴∠BGD′=60°,
∴∠FGE=∠BGD′=60°,
∵AD∥BC,
∴∠AFG=∠FGE=60°,
∴∠EFG=![]() (180°-∠AFG)=
(180°-∠AFG)=![]() (180°-60°)=60°,
(180°-60°)=60°,
∴△EFG是等边三角形,
∵AB=t,
∴EF=t÷![]() ,
,
∴△EFG的周长=![]() .
.
故答案为:![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目