��Ŀ����
����Ŀ����������ȫ��ͬ�Ŀ�Ƭ����A��B���飬ÿ�����ţ���A��Ŀ�Ƭ�Ϸֱ�����������B��Ŀ�Ƭ�Ϸֱ����������ͼ1��ʾ��
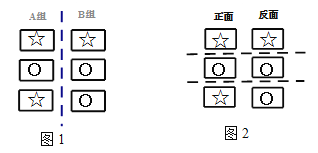
��1��������Ƭ�ޱ�ǵ�һ�泯�ϰ������ϣ����ֱ������鿨Ƭ���������ȡһ�ţ������ſ�Ƭ�ϱ�Ƕ������ĸ���������������ͼ�����б��������
��2������A��B���鿨Ƭ�ޱ�ǵ�һ���Ӧճ����һ��õ�3�ſ�Ƭ��������������ͼ2��ʾ������Ƭ���泯�ϰڷ������ϣ�����ƿ�Ǹ�ס��ǣ����ҿ����ӣ������Ŀ�Ƭ�����������������ķ���Ҳ��������¶Եĸ����Ƕ�����
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
�����������1���б��ó����еȿ��ܵ���������ҳ����ֿ�Ƭ�ϱ�Ƕ��ǡ�������������������������ĸ��ʣ�
��2�����еȿ��ܵ������2�֣����нҿ����ӣ������Ŀ�Ƭ�������ǡ����������ķ���Ҳ�ǡ������������1�֣��������������ʣ�
�����������1����������б����£�
�� | �� | �� | |
�� | ���������� | ���������� | ���������� |
�� | ���������� | ���������� | ���������� |
�� | ���������� | ���������� | ���������� |
�ӱ��п��Կ��������п��ܽ����9�֣���ÿ�ֽ�����ֵĿ�������ȣ��������ſ�Ƭ�ϱ�Ƕ������������2�֣����� P�����Ŷ�������=![]() ��
��
��2�����еȿ��ܵ������2�֣����нҿ����ӣ������Ŀ�Ƭ�������ǡ����������ķ���Ҳ�ǡ������������1�֣���P=![]() ��
��

 ��������������������ϵ�д�
��������������������ϵ�д�