题目内容
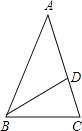
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
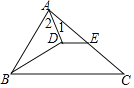
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
【答案】(1)见解析;(2)118°
【解析】
(1)如图延长AD交BC于E.证明△BDA≌△BDE(ASA)即可解决问题.
(2)求出∠AEC,再利用平行线的性质即可解决问题.
解:(1)如图延长AD交BC于E.

∵BD⊥AE,
∴∠BDA=∠BDE=90°,
∵∠ABD=∠EBD,BD=BD,
∴△BDA≌△BDE(ASA),
∴BA=BE,∠2=∠BEA,
∵∠BEA=∠1+∠C,
∴∠2=∠1+∠C.
(2)∵∠ABD=28°,∠BDA=90°,
∴∠2=62°,
∴∠AEB=∠2=62°,
∴∠AEC=180°﹣62°=118°,
∵DE∥EC,
∴∠ADE=∠AEC=118°.

练习册系列答案
相关题目