Question

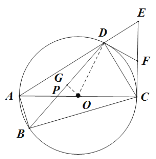
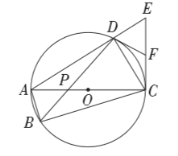
【题目】如图，四边形内接于，对角线是的直径，过点作的垂线交的延长线于点，为的中点，连接，，与交于点．

（1）求证：是的切线；

（2）若，求的值；

（3）若，，求的长．

Answer 1

【答案】（1）见解析；（2）2；（3）4

【解析】

（1）连接OD，证明，由F为CE中点，得DF=CF，结合OD=OC，证明，可得DF为的切线；

（2）证明△ACE∽△ADC，得AC2=AD·AE，可设DE=x（或DE=1），根据AC2=AD·AE求出AD，DC，，可得结果；

（3）过点O作于点G，根据垂径定理得BG=GD=m，表示PD=m+PG，PB=m-PG，根据，得，由得OG=PG，可得半径，即可得到AC．

解：（1）证明：如图，连接OD．

∵AC是⊙O的直径，

∴∠ADC=90°．

∴∠EDC=90°．

∵F是EC的中点，

∴DF=FC．

∴∠FDC=∠FCD．

∵OD=OC，

∴∠ODC=∠OCD．

∵AC⊥CE，

∴∠OCF=90°．

∴∠ODF=∠ODC＋∠FDC=∠OCD＋∠FCD=∠OCF=90°，即DF⊥OD．

∴DF是⊙O的切线．

（2）解：∵∠CAE＋∠E=90°，∠CAE＋∠ACD=90°，

∴∠E=∠ACD．

又∠ACE=∠ADC=90°，

∴△ACE∽△ADC．

∴，即AC2=AD·AE．

解法一：设DE=x，则AC=x，即（x）2=AD（AD+x）．

整理，得AD2＋AD·x－20x2=0．

解得AD=4x或AD=-5x（舍去）．

∴DC==2x．

∴tan∠ABD=tan∠ACD===2．

解法二：设DE=1，则AC=，即（）2=AD（AD+1）．

整理，得AD2＋AD－20=0．

解得AD=4或AD=-5（舍去）．

∴DC==2．

∴tan∠ABD=tan∠ACD==2．

（3）解：如图，过点O作于点G．

由垂径定理，得BG=DG．

设BG=DG=m，则PD=m+PG，PB=m-PG．

∵，

∴，整理，得，即．

∵∠DPC=45°，

∴OG=PG．

∴OD2=DG2+OG2=m2+PG2=4，即⊙O的半径为2．

∴AC=4．