题目内容
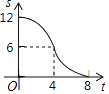
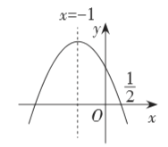
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() ,且过点
,且过点![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的结论是______.(填序号)
.其中正确的结论是______.(填序号)
【答案】①③⑤
【解析】
①由图像知![]() ; 由抛物线对称抽是
; 由抛物线对称抽是![]() 得
得![]() ,所以
,所以![]() ,
,![]() ;进而得
;进而得![]() ;
;
②有图像知,抛物线过![]() ,代入抛物线解析式可得
,代入抛物线解析式可得![]() ;
;
③由于![]() 可变形为
可变形为![]() , 而x轴上(
, 而x轴上(![]() ,0)关于
,0)关于![]() 对称的点是(
对称的点是(![]() ,0),所以
,0),所以![]() 正确;
正确;
④因为抛物线与x轴有两个不同的交点,所以![]() ;
;
⑤当![]() 时,抛物线取得最大值
时,抛物线取得最大值![]() ,当
,当![]() 时,则
时,则![]() ,整理可得
,整理可得![]() .
.
解:①由图像知![]() ; 由抛物线对称抽是
; 由抛物线对称抽是![]() 得
得![]() ,所以
,所以![]() ,
,![]() ;进而得
;进而得![]() ;故①正确;
;故①正确;
②有图像知,抛物线过![]() ,代入抛物线解析式整理可得
,代入抛物线解析式整理可得![]() ,故②错误;
,故②错误;
③由于![]() 可变形为
可变形为![]() , 而在x轴上(
, 而在x轴上(![]() ,0)关于
,0)关于![]() 对称的点是(
对称的点是(![]() ,0),故③正确;
,0),故③正确;
④由图像可知,抛物线与x轴有两个不同的交点,所以![]() ,故④错误;
,故④错误;
⑤当![]() 时,抛物线取得最大值
时,抛物线取得最大值![]() ,当
,当![]() 时,则
时,则![]() ,整理可得
,整理可得![]() .故⑤正确.
.故⑤正确.
故答案为:①③⑤.

练习册系列答案
相关题目