题目内容
【题目】某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
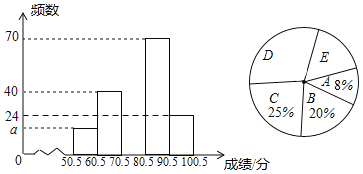
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
【答案】(1)200,16;(2)![]() ,图见解析;(3)估计成绩优秀的学生有1410名.
,图见解析;(3)估计成绩优秀的学生有1410名.
【解析】
(1)根据B小组的频数分布直方图和扇形统计图的信息可得样本容量,再利用样本容量乘以![]() 可得a的值;
可得a的值;
(2)先求出E小组所占的百分比,再乘以![]() 即可得n的值,利用(1)的结论,求出C小组的人数,再补全频数分布直方图即可;
即可得n的值,利用(1)的结论,求出C小组的人数,再补全频数分布直方图即可;
(3)先求出成绩在80分以上(不含80分)的人数占比,再乘以3000即可得.
(1)样本容量为![]()
则![]()
故答案为:200,16;
(2)E小组所占的百分比为![]()
则![]()
故n的值为![]()
C组的人数为![]() (人)
(人)
则补全频数分布直方图如下所示:
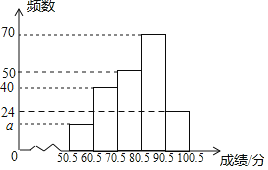
(3)成绩在80分以上(不含80分)的人数占比为D小组和E小组的占比之和
即![]()
则![]() (名)
(名)
答:估计成绩优秀的学生有1410名.

 名校课堂系列答案
名校课堂系列答案【题目】随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
拼单数x(单位:单) | 2 | 4 | 8 | 12 |
单价y(单位:元) | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m(单位:件) | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题:
(1)请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;
(2)拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?
(3)在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?