题目内容
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
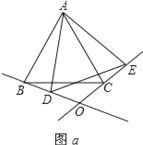
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
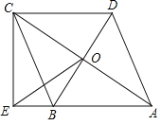
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .

【答案】(1)全等,理由见解析;(2)120°;(3)![]() .
.
【解析】
(1)结论:△ABD≌△ACE.根据SAS证明即可.
(2)利用全等三角形的性质解决问题即可.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.证明∠AOC=120°,推出点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°从而可以求得运动的轨迹.
解:(1)结论:△ABD≌△ACE.
∵△ADE是由△ABC绕点A旋转θ得到,∴△ABC是等边三角形.
∴AB=AD=AC=AE,∠BAD=∠CAE=20°,
在△ABD与△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
(2)由已知得:△ABC和△ADE是全等的等边三角形,∴AB=AD=AC=AE.
∵△ADE是由△ABC绕点A旋转θ得到的,∴∠BAD=∠CAE=θ.
∴△BAD≌△CAE(SAS).∴∠ADB=∠AEC.
∵∠ADB+∠ABD+∠BAD=180°,∴∠AEC+∠ABO+∠BAD=180°.
∵∠ABO+∠AEC+∠BAE+∠BOE=360°,∠BAE=∠BAD+∠DAE,
∴∠DAE+∠BOE=180°.
又∵∠DAE=60°,∴∠BOE=120°.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.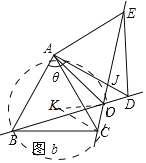
∵△ABD≌△ACE,
∴∠ODJ=∠AEJ,
∵∠AJE=∠OJD,
∴∠EAJ=∠JOD=60°,
∴∠AOC=120°,
∴点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°.
∴当θ从60°到120°的旋转过程中,运动的轨迹为![]() =
=![]() ,
,
故答案为:![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案