Question

【题目】如图1，四边形ABCD是正方形，动点P从点A出发，以2cm/s的速度沿边AB、BC、CD匀速运动到D终止；动点Q从A出发，以1cm/s的速度沿边AD匀速运动到D终止，若P、Q两点同时出发，运动时间为ts，△APQ的面积为Scm2 ． S与t之间函数关系的图象如图2所示．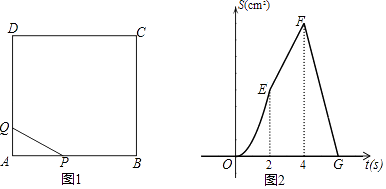

（1）求图2中线段FG所表示的函数关系式；
（2）当动点P在边AB运动的过程中，若以C、P、Q为顶点的三角形是等腰三角形，求t的值；
（3）是否存在这样的t，使PQ将正方形ABCD的面积恰好分成1：3的两部分？若存在，求出这样的t的值；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：由题意，可知题图2中点E表示点P运动至点B时的情形，

所用时间为2s，则正方形的边长AB=2×2=4cm．

点Q运动至点D所需时间为：4÷1=4s，点P运动至终点D所需时间为12÷2=6s．

因此在FG段内，点Q运动至点D停止运动，点P在线段CD上继续运动，且时间t的取值范围为4≤t≤6．

故S= ×4×（12﹣2t）=﹣4t+24，

∴FG段的函数表达式为S=﹣4t+24（4≤t≤6）．

（2）

解：①若CP=CQ，则DQ=PB，显然不成立

②若PC=PQ，则（4﹣2t）2+42=5t2，解得 ， （舍去）

③若QC=QP，则（4﹣t）2+42=5t2，解得t1=2，t2=﹣4（舍去）

综上所述，当 或t=2时，以C、P、Q为顶点的三角形是等腰三角形．

（3）

解：假设存在这样的t，使PQ将正方形ABCD的面积恰好分成1：3的两部分．

易得正方形ABCD的面积为16．

①当点P在AB上运动时，PQ将正方形ABCD分成△APQ和五边形PBCDQ两部分，

如图3所示，根据题意，得 ，解得t=2；

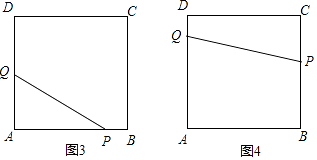
②当点P在BC上运动时，PQ将正方形ABCD分为梯形ABPQ和梯形PCDQ两部分，如图4所示．根据题意，得 （2t﹣4+t）×4= ×16，

解得t= ．

∴存在t=2和t= ，使PQ将正方形ABCD的面积恰好分成1：3的两部分．

【解析】（1）函数图象中线段FG，表示点Q运动至终点D之后停止运动，而点P在线段CD上继续运动的情形．求出S的表达式，并确定t的取值范围；（2）分CP=CQ、PC=PQ、QC=QP三种情况讨论即可确定答案；（3）当点P在AB上运动时，PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分，求出t的值；
当点P在BC上运动时，PQ将菱形分为梯形ABPQ和梯形PCDQ两部分，求出t的值．
【考点精析】解答此题的关键在于理解函数的图象的相关知识，掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值，以及对等腰三角形的性质的理解，了解等腰三角形的两个底角相等（简称：等边对等角）．