题目内容
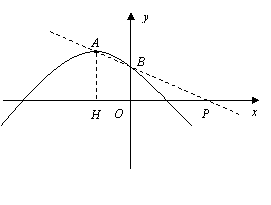
如图，抛物线
的顶点为A，与y 轴交于点B．
（1）求点A、点B的坐标．
（2）若点P是x轴上任意一点，求证：
．
（3）当
最大时，求点P的坐标．
 |
解：（1）抛物线
与y轴的交于点B，
令x=0得y=2．
∴B（0，2）
∵
∴A（―2，3）
（2）当点P是 AB的延长线与x轴交点时，
．
当点P在x轴上又异于AB的延长线与x轴的交点时，
在点P、A、B构成的三角形中，
．
综合上述：
（3）作直线AB交x轴于点P，由（2）可知：当PA―PB最大时，点P是所求的点
作AH⊥OP于H．
∵BO⊥OP，
∴△BOP∽△AHP
∴
由（1）可知：AH=3、OH=2、OB=2，
∴OP=4，故P（4，0）
注：求出AB所在直线解析式后再求其与x轴交点P（4，0）等各种方法只要正确也相应给分．
 |
练习册系列答案
相关题目
点．
21、如图，抛物线的顶点为A（1，-4），且过点B（3，0）．
（2013•河南）如图，抛物线的顶点为P（-2，2），与y轴交于点A（0，3）．若平移该抛物线使其顶点P沿直线移动到点P′（2，-2），点A的对应点为A′，则抛物线上PA段扫过的区域（阴影部分）的面积为
（2013•峨眉山市二模）已知，如图，抛物线的顶点为C（1，-2），直线y=kx+m与抛物线交于A、B两点，其中OA=3，B点在y轴上．点P为线段AB上的一个动点（点P与点A、B不重合），过点P且垂直于x轴的直线与这条抛物线交于点E．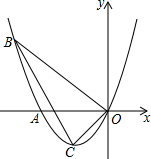
（2013•鄂尔多斯）如图，抛物线的顶点为C（-1，-1），且经过点A、点B和坐标原点O，点B的横坐标为-3．