题目内容
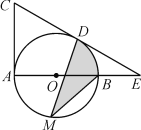
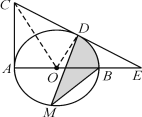
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,在⊙O上取点D,连接CD,使得AC=CD,延长CD交直线AB于点E.
(1)求证:CD是⊙O的切线.
(2)若AC=2![]() ,AE=6.
,AE=6.
①求⊙O的半径.
②点M是优弧![]() 上的一个动点(不与B,D重合),求MD,MB及弧BD围成的阴影部分面积的最大值.
上的一个动点(不与B,D重合),求MD,MB及弧BD围成的阴影部分面积的最大值.
【答案】(1)见解析;(2)①⊙O的半径为2,②![]() π+2
π+2
【解析】
(1)连结OD,OC.根据SSS可证△CAO≌△CDO,得∠ODC=∠OAC=90°,则CD是 O的切线;
(2)①由(1)的结论可以得到CD=CA,再依据勾股定理可以求得 O的半径为2;
②面积可看成两部分,三角形DMB跟弧DB的面积,弧DB不变,三角形面积为底DB乘以高除以2,当M运动到优弧![]() 的中点时,阴影部分的面积最大,可求得最大值.
的中点时,阴影部分的面积最大,可求得最大值.
(1)证明:连接OD,OC,如图.
∵AC是⊙O的切线,
∴∠CAB=90°,
在△CAO和△CDO中
 ,
,
∴△CAO≌△CDO.
∴∠CAO=∠CDO=90°,
∴CD⊥OD,
∴CD是⊙O的切线.
(2)解: ①∵AC=2![]() ,AE=6,
,AE=6,
∴根据勾股定理得:CE=4![]() ,
,
又∵AC=CD,∴DE=2![]() ,
,
∴∠CEA=30°,
∴tan∠CEA=![]() =
=![]() ,
,
∴OD=2.
∴⊙O的半径为2.
②∵图中阴影部分的面积可看成两部分,△DMB的面积和弓形DB的面积,
∵弧DB不变,∴三角形底边DB不变,
当M运动到优弧![]() 的中点,高最大,即面积最大.
的中点,高最大,即面积最大.
由(1)及第(2)①得:∠DOB=60°,当M运动到优弧![]() 的中点时,此时高经过圆心且垂直于DB,所以高的值为2+
的中点时,此时高经过圆心且垂直于DB,所以高的值为2+![]() ,
,
又△DOB是等边三角形,∴DB=OB=2,
∴S△DBM=![]() ×2×(2+
×2×(2+![]() )=2+
)=2+![]() ,
,
又因为S弓形DB=S扇形ODB-S△ODB=![]() -
-![]() =
=![]() -
-![]() ,
,
∴图中阴影部分的面积为:S=S弓形DB+S△DBM=![]() π+2.
π+2.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案