题目内容

【题目】若x1 ， x2 ， x3 ， x4 ， x5满足方程组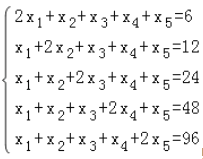则3x4+2x5的值是 ．

【答案】181
【解析】解：①+②+③+④+⑤得6x1+6x2+6x3+6x4+6x5=186
解得x1+x2+x3+x4+x5=31 ⑥
④﹣⑥得：x4=17，
⑤﹣⑥得：x5=65，
∴3x4+2x5=3×17+2×65=181．
所以答案是：181．
本题的方程组为对称轮换式，把5个方程相加得x1+x2+x3+x4+x5=31，要求x4、x5 ， 就分别与④⑤相减即可．
【考点精析】通过灵活运用解三元一次方程组，掌握通过“代入”或“加减”消元，把“三元”化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而转化为解一元一次方程即可以解答此题．

练习册系列答案
相关题目

【题目】如图，在△ABC中，AB=AC，AM是外角∠DAC的平分线．

（1）实践与操作：尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法），作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE．
（2）猜想并证明：∠EAC与∠DAC的数量关系并加以证明．

【题目】 （2016湖北鄂州第14题）如图，已知直线 与x轴、y轴相交于P、Q两点，与y=的图像相交于A（－2，m）、B（1，n）两点，连接OA、OB. 给出下列结论： ①k1k2<0；②m+n=0； ③S△AOP= S△BOQ；④不等式k1x+b＞的解集是x<－2或0<x<1，其中正确的结论的序号是 .

【题目】在平面直角坐标系中，将直线y＝－3x＋1向下平移4个单位长度后，所得直线的表达式为____________．

【题目】我市某重点中学校团委、学生会发出倡议，在初中各年级捐款购买书籍送给我市贫困地区的学校．初一年级利用捐款买甲、乙两种自然科学书籍若干本，用去5324元；初二年级买了A、B两种文学书籍若干本，用去4840元，其中A、B的数量分别与甲、乙的数量相等，且甲种书与B种书的单价相同，乙种书与A种书的单价相同．若甲、乙两种书的单价之和为121元，则初一和初二两个年级共向贫困地区的学校捐献了 本书．

【题目】2013年4月20日8时2分在四川省雅安市芦山县发生7.0级地震，有1.8万人等待安置，各地人民纷纷捐款灾区．某市一企业在得知灾区急需帐篷后立即与厂家联系购买帐篷送往灾区．已知用9万元刚好可以从厂家购进帐篷500顶．该厂家生产三种不同规格的帐篷，出厂价分别为甲种帐篷每顶150元，乙种帐篷每顶210元，丙种帐篷每顶250元．
①若企业同时购进其中两种不同规格的帐篷，则企业的购买方案有哪几种？
②若企业想同时购进三种不同规格的帐篷，必须每种帐篷都有，为了便于分类打包，每种帐篷数都要求是10的倍数．请你研究一下是否可行？如果可行请给出符合条件的设计方案；若不可行，请说明理由．

【题目】a+b=2，a2+b2=2，则ab的值为 ．

【题目】列方程（组）解应用题：
我市交通有关部门规定：出租车起步价允许行驶的最远路程为2千米，超过2千米的部分按每千米另收费．甲说：“我乘这种出租车走了11千米，表上显示要付费19.2元”；乙说：“我乘这种出租车走了20千米，表上显示要付费35.4元”．请你算一算这种出租车的起步价是多少元？以及超过2千米后每千米的车费是多少元？

【题目】某市举行“行动起来，对抗雾霾”为主题的植树活动，某街道积极响应，决定对该街道进行绿化改造，共购进甲、乙两种树共500棵，已知甲树每棵800元，乙树每棵1200元．
（1）若购买两种树总金额为560000元，求甲、乙两种树各购买了多少棵？
（2）若购买甲树的金额不少于购买乙树的金额，至少应购买甲树多少棵？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网