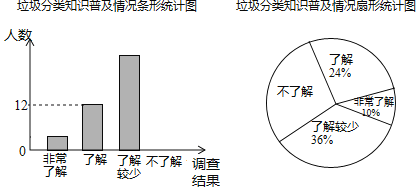
题目内容
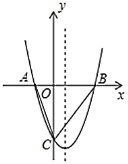
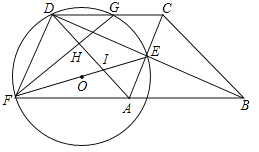
【题目】如图1:抛物线y=ax2+bx+3交x轴于点A、B,连接AC、BC,tan∠ABC=1,tan∠BAC=3.
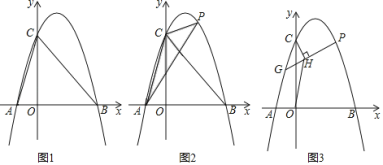
(1)求抛物线的解析式;
(2)如图2,点P在第一象限的抛物线上,连接PC、PA,若点P横坐标为t,△PAC的面积为S,求S与t的函数关系式;
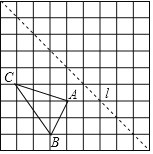
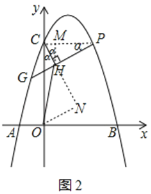
(3)在(2)的条件下,当S=3时,点G为第二象限抛物线上一点,连接PG,CH⊥PG于点H,连接OH,若tan∠OHG=![]() ,求GH的长.
,求GH的长.
【答案】(1)y=﹣x2+2x+3;(2)S=![]() t2+
t2+![]() t;(3)GH=
t;(3)GH=![]()
【解析】
(1)根据解析式得到OC=3,再根据已知条件求出点A、B的坐标即可求出解析式;
(2)根据点A、P的坐标求出直线AP的解析式,得到直线与y轴交点R的坐标,即可求出S与t的函数关系式;
(3)先求出点P的坐标得到CP∥x轴,作CH⊥GP,作HM⊥CP,过点O作ON⊥CH交CH的延长线于点N,分别求出CH、ON、CN,根据tan∠OHG=![]() 求出点H的坐标,根据直线PG求出点G的坐标,即可得到答案.
求出点H的坐标,根据直线PG求出点G的坐标,即可得到答案.
解:(1)由题意得c=3,∴OC=3,
∵tan∠ABC=1,∴OB=3,
∵tan∠BAC=3,∴OA=1,
∴点A、B、C的坐标分别为:(﹣1,0)、(3,0)、(0,3),
则抛物线的表达式为:y=a(x+1)(x﹣3),
将点C坐标代入上式并解得:a=﹣1,
∴抛物线的表达式为:y=﹣x2+2x+3;
(2)点P(t,﹣t2+2t+3),点A(﹣1,0),

将点P、A坐标代入一次函数表达式y=kx+b并解得:
直线PA的表达式为:y=(3﹣t)(x+1),
设直线AP交y轴于点R,则R(0,3﹣t),
S=![]() CR×(xP﹣xA)=
CR×(xP﹣xA)=![]() (3﹣3+t)(t+1)=
(3﹣3+t)(t+1)=![]() t2+
t2+![]() t;
t;
(3)S=![]() t2+
t2+![]() t=3,解得:t=﹣3(舍去)或2,
t=3,解得:t=﹣3(舍去)或2,
∴点P(2,3),
∵点C(0,3),
连接CP,则CP∥x轴,
作CH⊥GP,则∠CPH=∠OCH=α,
作HM⊥CP,则∠CHM=∠HCO=α,
过点O作ON⊥CH交CH的延长线于点N,
CP=2,OC=3,
CH=CPsinα=2sinα,ON=OCsinα=3sinα,CN=OCcosα=3cosα,
∵ON⊥CN,GH⊥CH,
∴∠HON=∠OHG,
∴tan∠HON=![]() =tan∠OHG=
=tan∠OHG=![]() ,
,
解得:tan![]() ,则sinα=
,则sinα=![]() ,cosα=
,cosα=![]() ,
,
MH=CHcosα=2sinαcosα=![]() ,CM=CHsinα=
,CM=CHsinα=![]() ,
,
∴点H(![]() ,
,![]() );
);
设点G(m,﹣m2+2m+3),而点P(2,3),
由点G、P的坐标得,直线PG表达式中的k值为:﹣m=﹣tanα=-![]() ,
,
∴点G(﹣![]() ,
,![]() ),
),
由点G、H的坐标得,GH=![]() .
.

 天天练口算系列答案
天天练口算系列答案