题目内容
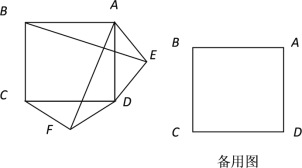
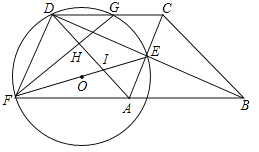
【题目】如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.
(1)求∠FDE的度数;
(2)试判断四边形FACD的形状,并证明你的结论;
(3)当G为线段DC的中点时,
①求证:FD=FI;
②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.
【答案】(1)90°;(2)四边形FACD是平行四边形;(3)①证明见试题解析;②![]() .
.
【解析】
试题(1)根据圆周角定理即可得到∠FDE=90°;
(2)由四边形ABCD是菱形,得到AB∥CD,AC⊥BD,∠AEB=90°,又由∠FDE=90°,得到∠AEB=∠FDE,从而有AC∥DF,故故可得到结论;
(3)①连接GE,易证GE是△ACD的中位线,即可得到GE∥DA,即可得到∠FHI=∠FGE=∠FGE=90°.由直角三角形斜边上的中线等于斜边的一半可得DG=GE,从而有![]() ,由圆周角定理可得∠1=∠2,再根据等角的余角相等可得∠3=∠4,进一步由等角对等边可得FD=DI;
,由圆周角定理可得∠1=∠2,再根据等角的余角相等可得∠3=∠4,进一步由等角对等边可得FD=DI;
②易知S⊙O=![]() ,S菱形ABCD=2mn,易证EI=EA=m,DF=AC=2m,EF=FI+IE=DF+AE=3m,在Rt△DEF中运用勾股定理即可解决问题.
,S菱形ABCD=2mn,易证EI=EA=m,DF=AC=2m,EF=FI+IE=DF+AE=3m,在Rt△DEF中运用勾股定理即可解决问题.
试题解析:(1)∵EF是⊙O的直径,∴∠FDE=90°;
(2)四边形FACD是平行四边形.理由如下:
∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴∠AEB=90°,又∵∠FDE=90°,∴∠AEB=∠FDE,∴AC∥DF,∴四边形FACD是平行四边形;
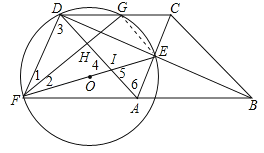
(3)①连接GE,如图.∵四边形ABCD是菱形,∴点E为AC中点,∵G为线段DC的中点,∴GE∥DA,∴∠FHI=∠FGE,∵EF是⊙O的直径,∴∠FGE=90°,∴∠FHI=90°,∵∠DEC=∠AEB=90°,G为线段DC的中点,∴DG=GE,∴![]() ,∴∠1=∠2.∵∠1+∠3=90°,∠2+∠4=90°,∴∠3=∠4,∴FD=FI;
,∴∠1=∠2.∵∠1+∠3=90°,∠2+∠4=90°,∴∠3=∠4,∴FD=FI;
②∵AC∥DF,∴∠3=∠6,∵∠4=∠5,∠3=∠4,∴∠5=∠6,∴EI=EA,∵四边形ABCD是菱形,四边形FACD是平行四边形,∴DE=![]() BD=n,AE=
BD=n,AE=![]() AC=m,FD=AC=2m,∴EF=FI+IE=FD+AE=3m,在Rt△EDF中,根据勾股定理可得:
AC=m,FD=AC=2m,∴EF=FI+IE=FD+AE=3m,在Rt△EDF中,根据勾股定理可得:![]() ,即
,即![]() ,∴S⊙O=
,∴S⊙O=![]() =
=![]() ,S菱形ABCD=
,S菱形ABCD=![]() ,∴S⊙O:S菱形ABCD=
,∴S⊙O:S菱形ABCD=![]() .
.

 出彩同步大试卷系列答案
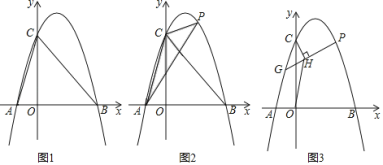
出彩同步大试卷系列答案【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
【题目】为迎接市教育局开展的“学雷锋·做有道德的人”主题演讲活动,某区教育局团委组织各校学生进行演讲预赛,然后将所有参赛学生的成绩 (得分为整数,满分为100分) 分成四组,绘制了不完整的统计图表如下:
组别 | 成绩x | 组中值 | 频数 |
第一组 | 90≤x≤100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | |
第三组 | 70≤x<80 | 75 | 8 |
第四组 | 60≤x<70 | 65 |
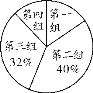
观察图表信息,解答下列问题:
(1)参赛学生共有 人,补全表格;
(2)如果将各组的组中值视为该组的平均成绩,请你估计所有参赛学生的平均成绩;
(3)小娟说: “根据以上统计图表, 我可以确定所有参赛学生成绩的中位数在哪一组,但不能确定众数在哪一组?”你同意她的观点吗?请说明理由.
(4)成绩落在第一组的恰好是两男两女四位学生,区教育局团委从中随机挑选两位学生参加市教育局组织的决赛,通过列表或画树状图的方法求出挑选的两位学生恰好是一男一女的概率.