题目内容
【题目】图
、图
分别是
的网格，网格中的每个小正方形的边长均为1，点
、
、
、
在小正方形的顶点上．请在网格中按要求画出图形：
（1）在图中画以
为斜边的直角三角形
（点
在小正方形的顶点上），使得
；
（2）在图中画以
为边的四边形
（点
、
在小正方形的顶点上），使得四边形是中心对称图形但不是轴对称图形，且
，并直接写出四边形的面积．
【答案】（1）见解析；（2）画图见解析；S四边形CDMN=6．
【解析】
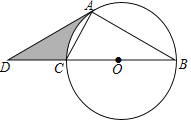
（1）根据题意可知：AB=5，因为
、2、5恰好构成以AB为斜边的直角三角形，由此画出图形即可；
（2）先根据轴对称图形和中心对称图形图形的性质，再利用锐角三角函数关系在网格中画出一平行四边形，然后求出这个四边形的面积．
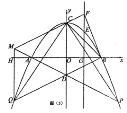
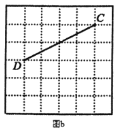
（1）如图a所示，△ABE即为所求
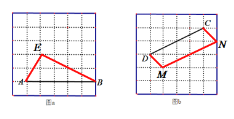
（2）如图b所示，四边形CDMN即为所求
∵S四边形CDMN=5×3-
=6
∴S四边形CDMN=6
灵星计算小达人系列答案
【题目】在新的教学改革的推动下，某中学初三年级积极推进走班制教学．为了了解一段时间以来“至善班”的学习效果，年级组织了多次定时测试，现随机选取甲、乙两个“至善班”，从中各抽取20名同学在某一次定时测试中的数学成绩，其结果记录如下：
收集数据：
“至善班”甲班的20名同学的数学成绩统计(满分为100分)(单位：分)：86 90 60 76 92 83 56 76 85 70 96 96 90 68 78 80 68 96 85 81
“至善班”乙班的20名同学的数学成绩统计(满分为100分)(单位：分)：78 96 75 76 82 87 60 54 87 72 100 82 78 86 70 92 76 80 98 78
整理数据：(成绩得分用x表示)
分数 数量 班级 | 0≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x＜100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据，并回答下列问题：
（1）完成下表：
平均数 | 中位数 | 众数 | |
甲班 | 80.6 | 82 | a＝ |
乙班 | 80.35 | b＝ | 78 |
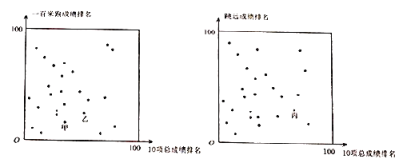
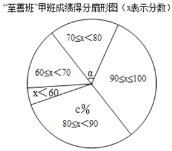
（2）在“至善班”甲班的扇形图中，成绩在70≤x＜80的扇形中，所对的圆心角α的度数为 ，估计全部“至善班”的1600人中优秀人数为 人．(成绩大于等于80分为优秀)
（3）根据以上数据，你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些，你所做判断的理由是：① ；② ．