题目内容
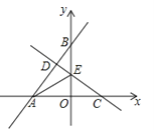
【题目】 如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A是(1,1),点C(a,b),满足![]() .
.
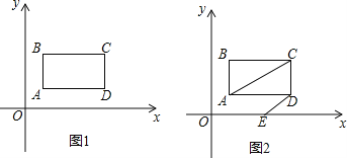
(1)求长方形ABCD的面积;
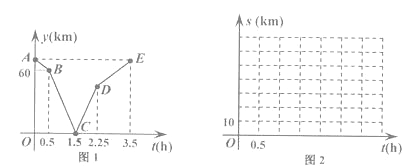
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发,沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=5时,求三角形OMC的面积;
②若AC∥ED,求t的值.
【答案】(1)8;(2)①4;②3
【解析】
(1)由已知得出a=5,b=3,求得C点坐标,结合图象,能找出其它几点的坐标,从而能得出长方形ABCD的面积;
(2)①拆分三角形,求出各个图形的面积即可求得;
②过点A作AF∥CD,交x轴于点M,交DE的延长线于点F,根据平行四边形的性质可得出AF的长度,结合AM的长度可得出ME为△FAD的中位线,根据点M、A的运动速度可得出关于t的一元一次方程,解之即可得出结论.
解:(1)∵![]() .
.
∴a-5=0,b-3=0,即a=5,b=3,
∵四边形ABCD为长方形,
∴点B(1,3),点C(5,3),点D(5,1),
∴AB=3-1=2,BC=5-1=4,
长方形ABCD的面积为:AB×BC=2×4=8;
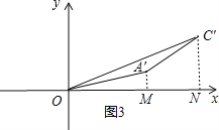
(2)①将t=5时,线段AC拿出来,放在图3中,各字母如图,
∵点A′(6,1),点C′(10,3),
∴OM=6,ON=10,A′M=1,C′N=3,MN=ON-OM=4,
∴三角形OA′C′的面积=![]() ONC′N-
ONC′N-![]() OMA′M-
OMA′M-![]() (A′M+C′N)MN=15-3-8=4;
(A′M+C′N)MN=15-3-8=4;
即三角形OMC的面积为4;
②过点A作AF∥CD,交x轴于点M,交DE的延长线于点F,
如图4所示,
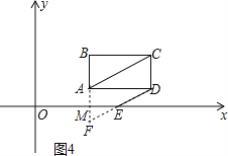
∵AF∥CD,AC∥DF,
∴四边形AFDC为平行四边形,
∴AF=CD=2.
∵AM=1,
∴ME为△FAD的中位线,
∴ME=![]() AD=2,
AD=2,
即2t-(t+1)=2,
解得:t=3.
故若AC∥ED,t的值为3秒.