题目内容
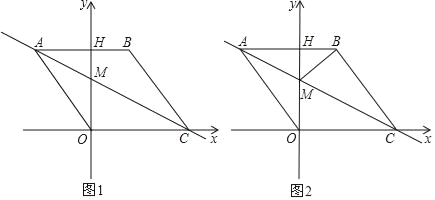
【题目】如图,直线l1:![]() 分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:
分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:![]() 经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
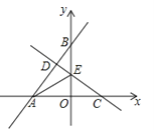
(1)当点C的坐标为![]() 时,①求直线l2的函数表达式;②求证:AE平分
时,①求直线l2的函数表达式;②求证:AE平分![]() ;
;
(2)问:是否存在点C,使![]() 是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
【答案】(1)①![]() ;②答案见解析;(2)存在点C使
;②答案见解析;(2)存在点C使![]() 是以CE为一腰的等腰三角形, 点C的坐标为(3,0)或(8,0).
是以CE为一腰的等腰三角形, 点C的坐标为(3,0)或(8,0).
【解析】
(1)①由点C的坐标,利用待定系数法即可求出b值,此题得解;
②利用一次函数图象上点的坐标特征可求出点A、E的坐标,利用勾股定理以及两点间的距离即可求出AC=AB,由正切的定义即可得出∠ABO=∠ACD,结合公共角即可利用全等三角形的判定定理ASA证出△ABO≌△ACD,从而得出AO=AD、∠ADC=∠AOB=90°,再利用全等直角三角形的判定定理HL即可证出Rt△ADE≌Rt△AOE,根据全等三角形的性质可找出∠DAE=∠OAE,由此即可证出AE平分∠BAC;
(2)△ACE是以CE为一腰的等腰三角形分两种情况:①CE=AE时,利用等腰三角形的性质结合点A的坐标即可得出点C的坐标;②当CA=CE时,设点C(m,0)(m>0),则OC=m,OE=![]() OC=
OC=![]() m,CA=m+2,利用勾股定理求出CE,由CA=CE即可得出关于m的一元一次方程,解之即可得出点C的坐标.综上即可得出结论.
m,CA=m+2,利用勾股定理求出CE,由CA=CE即可得出关于m的一元一次方程,解之即可得出点C的坐标.综上即可得出结论.
(1)①将C(2,0)代入y=![]() ,0=
,0=![]() ,解得:
,解得: ![]() ,
,
∴直线l2的函数表达式为![]() .
.
②证明:当![]() 时,x=3,
时,x=3,
∴点A(3,0),
∴![]() ,
,![]() ,AC=2(3)=5=AB.
,AC=2(3)=5=AB.
∵当x=0时![]() ,
,
∴![]() ,
,
∴∠ABO=∠ACD.
在△ABO和△ACD中,
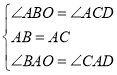 ,
,
∴△ABO≌△ACD(ASA),
∴![]() .
.
在Rt△ADE和Rt△AOE中,
![]() ,
,
∴Rt△ADE≌Rt△AOE(HL),
∴∠DAE=∠OAE,
∴AE平分∠BAC.
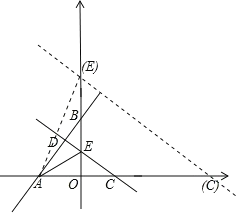
(2)△ACE是以CE为一腰的等腰三角形分两种情况:
①当AE=CE时,
∵EO⊥AC,
∴OC=OA,
∴点C(3,0);
②当CA=CE时,设点C(m,0)(m>0),则![]() ,CA=m+2,
,CA=m+2,
∴![]() ,
,
∴![]() ,
,
解得:m=8,
∴点C(8,0).
综上所述:存在点C,使△ACE是以CE为一腰的等腰三角形,点C的坐标为(3,0)或(8,0).